
 ��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��-4��1���������߽�y����A�㣬��x����B��C���㣨��B��C���Ҳࣩ����֪A������Ϊ��0��-3����
��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��-4��1���������߽�y����A�㣬��x����B��C���㣨��B��C���Ҳࣩ����֪A������Ϊ��0��-3�������� ��1���趥��ʽy=a��x+4��2+1��Ȼ���A������������a���ɣ�
��2����ȷ��C��-6��0����B��-2��0����A��0��-3�����ټ����AB=$\sqrt{13}$����CF��BD��D����ͼ������֤��Rt��BCF��Rt��ABO���������Ʊȼ����CF=$\frac{8\sqrt{13}}{13}$��Ȼ��������C��ֱ��l�ľ��룬�Ӷ��ɸ���ֱ����Բ��λ�ù�ϵ���ж������ж������ߵĶԳ���l���C��λ�ù�ϵ��
��3����PQ��y�ύAC��Q����ͼ�������ô���ϵ�������ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x-3����P��t��-$\frac{1}{4}$t2-2t-3������Q��t��-$\frac{1}{2}$t-3������-6��t��0������PQ=-$\frac{1}{4}$t2-$\frac{3}{2}$t=-$\frac{1}{4}$��t-3��2+$\frac{9}{4}$�������������������ʽ�õ�S��PAC=-$\frac{3}{4}$��t-3��2+$\frac{27}{4}$��Ȼ�����ö��κ��������ʽ�����⣮
��� �⣺��1���������ߵĽ���ʽΪy=a��x+4��2+1
��A��0��-3�������16a+1=-3�����a=-$\frac{1}{4}$��
���������߽���ʽΪy=-$\frac{1}{4}$��x+4��2+1����y=-$\frac{1}{4}$x2-2x-3��
��2�������ߵĶԳ���l���C�ཻ���������£�
��y=0ʱ��-$\frac{1}{4}$��x+4��2+1=0�����x1=-2��x2=-6����C��-6��0����B��-2��0������
��x=0ʱ��y=-$\frac{1}{4}$��x+4��2+1=-3����A��0��-3����
��AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$��
��CF��BD��D����ͼ��
��AB��BD��
���ABO+��FBC=90�㣬
����ABO+��OAB=90�㣬
���FBC=��OAB��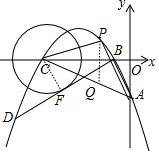
��Rt��BCF��Rt��ABO��
��CF��OB=BC��AB����CF��2=4��$\sqrt{13}$�����CF=$\frac{8\sqrt{13}}{13}$��
�������ߵĶԳ���Ϊֱ��x=-4��
���C��ֱ��l�ľ���Ϊ-4-��-6��=2��
��$\frac{8\sqrt{13}}{13}$��2��
�������ߵĶԳ���l���C�ཻ��
��3����PQ��y�ύAC��Q����ͼ��
��ֱ��AC�Ľ���ʽΪy=kx+b��
��C��-6��0����A��0��-3�������$\left\{\begin{array}{l}{-6k+b=0}\\{b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{1}{2}$x-3��
��P��t��-$\frac{1}{4}$t2-2t-3������Q��t��-$\frac{1}{2}$t-3������-6��t��0��
��PQ=-$\frac{1}{4}$t2-2t-3-��-$\frac{1}{2}$t-3��=-$\frac{1}{4}$t2-$\frac{3}{2}$t=-$\frac{1}{4}$��t-3��2+$\frac{9}{4}$��
��S��PAC=$\frac{1}{2}$•PQ•6=3PQ=-$\frac{3}{4}$��t-3��2+$\frac{27}{4}$��
��t=3ʱ����PAC�����������ֵΪ$\frac{27}{4}$����ʱP������Ϊ��-3��$\frac{3}{4}$����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ��������ʺ����������ε��ж������������ô���ϵ������������ʽ��ѧ���ù��ɶ������涨��֤��ֱ�������Σ�����������ͼ�����ʣ���ס�����ľ��빫ʽ�������÷������۵�˼������ѧ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC��
��ͼ����ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=2��BC=2$\sqrt{3}$��D��BC����һ�㣬ֱ��ED��BC�ڵ�D����AB�ڵ�E��CF��AB��ֱ��DE�ڵ�F����CD=x
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=2��BC=2$\sqrt{3}$��D��BC����һ�㣬ֱ��ED��BC�ڵ�D����AB�ڵ�E��CF��AB��ֱ��DE�ڵ�F����CD=x�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
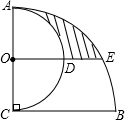 ��ͼ��AC��BC��AC=BC=4����ACΪֱ������Բ��Բ��Ϊ��O���Ե�CΪԲ�ģ�BCΪ�뾶����AB������O��BC��ƽ���߽������ڵ�D��E������Ӱ���ֵ�����ǣ�������
��ͼ��AC��BC��AC=BC=4����ACΪֱ������Բ��Բ��Ϊ��O���Ե�CΪԲ�ģ�BCΪ�뾶����AB������O��BC��ƽ���߽������ڵ�D��E������Ӱ���ֵ�����ǣ�������| A�� | $\frac{5}{3}��-2\sqrt{3}$ | B�� | $\frac{5}{3}��-4$ | C�� | $3��-2\sqrt{3}$ | D�� | 3��-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com