
 的度数.
的度数.
 =
= =
= 而它们的和为半圆,即可求出
而它们的和为半圆,即可求出 的度数.
的度数.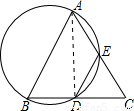 解:(1)如图:连接AD,
解:(1)如图:连接AD, =
= =
=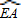 ,
, 的度数为
的度数为 ×180°=60°.
×180°=60°.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
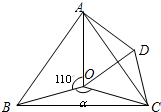 24、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
24、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:
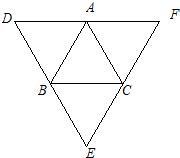
 如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,那么,四边形AFED是否为平行四边形?如果是,请证明之,如果不是,请说明理由.
如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,那么,四边形AFED是否为平行四边形?如果是,请证明之,如果不是,请说明理由.查看答案和解析>>
科目:初中数学 来源:2006年初中数学总复习下册 题型:047
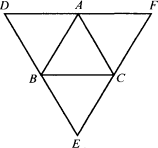
已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.
(1)如图,当△ABC是等边三角形时,请你写出满足图中条件,四个成立的结论;
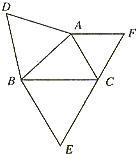
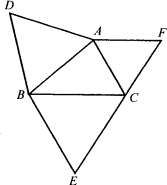
(2)如图,当△ABC中只有∠ACB=60°时,请你证明S△ABC与S△ABD的和等于S△BCE与S△ACE的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com