
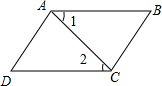
 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠B=∠D;④∠D=∠ACB,其中正确的有①②③.
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠B=∠D;④∠D=∠ACB,其中正确的有①②③. 分析 ①根据内错角相等,判定两直线平行;
②根据两直线平行,同旁内角互补与同旁内角互补,两直线平行进行判定;
③根据两直线平行,同旁内角互补与同角的补角相等判定;
④∠D与∠ACB不能构成三线八角,无法判断.
解答 解:∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行),
所以①正确;
∵AB∥CD(已证),
∴∠BAD+∠ADC=180°(两直线平行,同旁内角互补),
又∵∠BAD=∠BCD,
∴∠BCD+∠ADC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
故②也正确;
∵AB∥CD,AD∥BC(已证),
∴∠B+∠BCD=180°,
∠D+∠BCD=180°,
∴∠B=∠D(同角的补角相等),
所以③也正确;
只有当AB=AC时才会有∠B=∠ACB=∠D,
所以④不正确.
故答案为①②③.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定是解题的关键,即①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
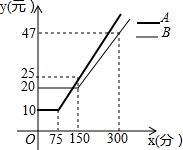 某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.
某通讯公司推出A、B两种手机话费套餐,这两种套餐每月都有一定的固定费用和免费通话时间,超过免费通话时间的部分收费标准为:A套餐a元/分,B套餐b元/分,使用A、B两种套餐的通话费用y(元)与通话时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
| 桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平面直角坐标系中,已知点B(2,1),过点B作BA⊥x轴,垂足为A,若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,平面直角坐标系中,已知点B(2,1),过点B作BA⊥x轴,垂足为A,若抛物线y=$\frac{1}{2}$x2+k与△OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -2<k<0 | B. | -2<k<$\frac{1}{8}$ | C. | -2<k<-1 | D. | -2<k<$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com