
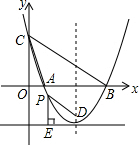
 ��֪������y=$\frac{1}{2}$x2+2��m+1��x-m+1��x�ύ�ڵ�A��B����y�ύ�ڵ�C����Գ�����ֱ��x=4��
��֪������y=$\frac{1}{2}$x2+2��m+1��x-m+1��x�ύ�ڵ�A��B����y�ύ�ڵ�C����Գ�����ֱ��x=4������ ��1���ɶԳ���x=-$\frac{b}{2a}$�����m����ֵ���ó���������ʽ���ٽ�һ����ö������꼴�ɣ�
��2����x=0�����y�ύ��C�����꣬��y=0�ó���x�ύ���A��B�������꣬��һ����á�ABC��������ɣ�
��3�������P�����꣬��������֮��ľ������PE��PD���������̣����t����ֵ������ڣ������ڣ�
��� �⣺��1����x=-2��m+1��=4��
���m=-3��
���������߽���ʽΪy=$\frac{1}{2}$x2-4x+4����������Ϊ��4��-4����
��2��������y=$\frac{1}{2}$x2-4x+4��y�ύ�ڵ�C������Ϊ��0��4����
��y=$\frac{1}{2}$x2-4x+4=0��
��ã�x1=4+2$\sqrt{2}$��x2=4-2$\sqrt{2}$��
��A��������4-2$\sqrt{2}$��0����B��������4+2$\sqrt{2}$��0����
��ˡ�ABC�����=$\frac{1}{2}$��4��4$\sqrt{2}$=8$\sqrt{2}$��
��3������������tֵ��ʹ��������������һ��P��a��b��������ֱ�ߵľ������P�㵽D��ľ��룮
��P���������m��$\frac{1}{2}$m2-4m+4������D��4��t+1����
PE=$\frac{1}{2}$m2-4m+4-t��
PD=$\sqrt{��4-m��^{2}+[t+1-��\frac{1}{2}{m}^{2}-4m+4��]^{2}}$
��$\frac{1}{2}$m2-4m+4-t=$\sqrt{��4-m��^{2}+[t+1-��\frac{1}{2}{m}^{2}-4m+4��]^{2}}$��
��ã�t=-$\frac{9}{2}$��
��˵�t=-$\frac{9}{2}$ʹ��������������һ��P��a��b��������ֱ�ߵľ������P�㵽D��ľ��룮
���� ���⿼����κ������ۺ����⣬����ϵ���������Ľ���ʽ��������Ľ������꣬����֮��ľ��빫ʽ��ע�����ν��˼������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
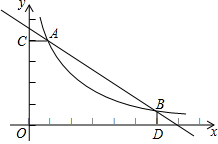 ��ͼ����֪��A��1��4������B��6��$\frac{2}{3}$����һ�κ���y=kx+bͼ���뷴��������y=$\frac{m}{x}$��m��0��ͼ��Ľ��㣬AC��y���ڵ�C��BD��x���ڵ�D��
��ͼ����֪��A��1��4������B��6��$\frac{2}{3}$����һ�κ���y=kx+bͼ���뷴��������y=$\frac{m}{x}$��m��0��ͼ��Ľ��㣬AC��y���ڵ�C��BD��x���ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
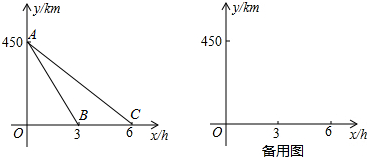
 �ס���������һ����Ϊ500m��ֱ���ܵ���ͬ��㡢ͬ�������ܲ�����֪���ȳ���2s�����ٳ������ȵ��յ����ԭ����Ϣ����ͼ��ʾ���Ǽס�������֮��ľ���y��m�����ҳ�����ʱ��t��s���ĺ�����ϵ���������½��ۣ���a=8����b=92����c=23��������ȷ���ǣ�������
�ס���������һ����Ϊ500m��ֱ���ܵ���ͬ��㡢ͬ�������ܲ�����֪���ȳ���2s�����ٳ������ȵ��յ����ԭ����Ϣ����ͼ��ʾ���Ǽס�������֮��ľ���y��m�����ҳ�����ʱ��t��s���ĺ�����ϵ���������½��ۣ���a=8����b=92����c=23��������ȷ���ǣ�������| A�� | �٢ڢ� | B�� | �٢� | C�� | �٢� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij��ѧ�ۺ�ʵ��С��ͬѧ�����������ɽ�������ĸ߶ȣ�������ɽ���µ�D�����ɽ��B������Ϊ30�㣬����ɽ����ǰ����4�״ﵽE������ù�������ͷ��A�����Ϊ45�㣬��֪����ɽ��ɽ�������ı�ߣ��߶�BC�ij��ȣ�Ϊ60�ף������������ĸ߶�Ϊ�����ף��������ȷ��0.1�ף�$\sqrt{3}$��1.73��
ij��ѧ�ۺ�ʵ��С��ͬѧ�����������ɽ�������ĸ߶ȣ�������ɽ���µ�D�����ɽ��B������Ϊ30�㣬����ɽ����ǰ����4�״ﵽE������ù�������ͷ��A�����Ϊ45�㣬��֪����ɽ��ɽ�������ı�ߣ��߶�BC�ij��ȣ�Ϊ60�ף������������ĸ߶�Ϊ�����ף��������ȷ��0.1�ף�$\sqrt{3}$��1.73���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
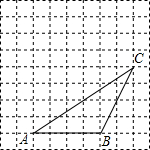 ��ͼ����ABC�Ķ��㶼�ڷ���ֽ�ĸ���ϣ�����ABC����ƽ��1��������ƽ��3������ÿ�����ӵı߳�Ϊ1����λ���ȣ�
��ͼ����ABC�Ķ��㶼�ڷ���ֽ�ĸ���ϣ�����ABC����ƽ��1��������ƽ��3������ÿ�����ӵı߳�Ϊ1����λ���ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ȱ�������ABC�У���D��E�ֱ�ΪAB��AC���е㣬���DEC�Ķ���Ϊ��������
��ͼ���ȱ�������ABC�У���D��E�ֱ�ΪAB��AC���е㣬���DEC�Ķ���Ϊ��������| A�� | 150�� | B�� | 120�� | C�� | 60�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx-2����A��B�����㣨��A�ڵ�B����ࣩ����y���ڵ�C����֪A��-1��0����B��3��0����
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx-2����A��B�����㣨��A�ڵ�B����ࣩ����y���ڵ�C����֪A��-1��0����B��3��0�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com