练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

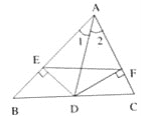
    【题目】已知，如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高。求证：AD垂直平分EF。

    【答案】见解析

    【解析】

    由DE⊥AB,DF⊥AC，得出∠AED=∠AFD；因为AD是△ABC的角平分线，可得∠1=∠2，DE=DF，推出△AED≌△AFD，即AE=AF，所以点A在EF的垂直平分线上，又DE=DF，推出点D在EF的垂直平分线上，即可证明AD垂直平分EF；

    证明：∵DE⊥AB，DF⊥AC，

    ∴∠AED=∠AFD，

    又∵AD是△ABC的角平分线，

    ∴∠1=∠2，DE=DF，

    ∴△AED≌△AFD（AAS），

    ∴AE=AF，

    ∴点A在EF的垂直平分线上（到线段两端距离相等的点在线段的垂直平分线上），

    ∵DE=DF，

    ∴点D在EF的垂直平分线上，

    ∴AD垂直平分EF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某文具店某几种型号的计算器每只进价 12 元、售价 20 元，多买优惠， 优惠方法是：凡是一次买 10 只以上的，每多买一只，所买的全部计算器每只就 降价 0.1 元，例如：某人买 18 只计算器，于是每只降价 0.1×(18－10)＝0.8(元)， 因此所买的 18 只计算器都按每只 19.2 元的价格购买，但是每只计算器的最低售 价为 16 元．

    (1)求一次至少购买多少只计算器，才能以最低售价购买？ (2)写出该文具店一次销售 x(x＞10)只时，所获利润 y(元)与 x(只)之间的函数关系 式，并写出自变量 x 的取值范围；

    (3)一天，甲顾客购买了 46 只，乙顾客购买了 50 只，店主发现卖 46 只赚的钱反 而比卖 50 只赚的钱多，请你说明发生这一现象的原因；当 10＜x≤50 时，为了 获得最大利润，店家一次应卖多少只？这时的售价是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，，若，则还需添加的一个条件有( )

    A.种B.种C.种D.种

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】商场销售服装，平均每天可售出件，每件盈利元，为扩大销售量，减少库存，该商场决定采取适当的降价措施，经调查发现，一件衣服降价元，每天可多售出件．

    设每件降价元，每天盈利元，请写出与之间的函数关系式；若商场每天要盈利元，同时尽量减少库存，每件应降价多少元？

    每件降价多少元时，商场每天盈利达到最大？最大盈利是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，AB=AC，点D，E在边BC上，且BD=CE.

    (1)求证: △ABD≌△ACE；

    (2)若∠B=40°，AB=BE，求∠DAE的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交AC于点D，动点P在抛物线对称轴上，动点Q在抛物线上．

    （1）求抛物线的解析式；

    （2）当PO+PC的值最小时，求点P的坐标；

    （3）是否存在以A，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出P，Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“校园安全”受到全社会的广泛关注，东营市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

    （1）接受问卷调查的学生共有_______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°；

    （2）请补全条形统计图；

    （3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

    （4）若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在第一个△ABA中，∠B=20°，AB=AB，在AB上取一点C，延长AA到A，使得AA=AC，得到第二个△AAC；在AC上取一点D，延长AA到A，使得AA=AD；…，按此做法进行下去，则第5个三角形中，以点A4为顶点的底角的度数为（ ）

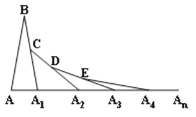
    A.5°B.10°C.170°D.175°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店两次购进一批同型号的热水壶和保温杯，第一次购进 12 个热水壶和 15 个保温杯，共用去资金 2850 元，第二次购进 20 个热水壶和 30 个保温杯，用去资金 4900元（购买同一商品的价格不变）

    （1）求每个热水壶和保温杯的采购单价各是多少元?

    （2）若商场计划再购进同种型号的热水壶和保温杯共 80 个，求所需购货资金 w（元） ，购买热水壶的数量 m(个)的函数表达式.

    （3）在（2）的基础上，若准备购买保温杯的数量是热水壶数量的 3 倍，则该商店需要准备多少元的购货资金?

    查看答案和解析>>

    同步练习册答案