
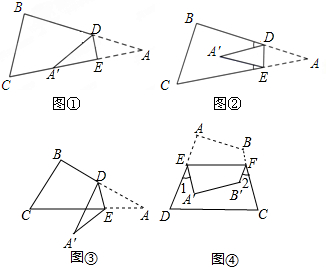
分析 (1)先根据折叠性质得∠A=∠AA′D,然后根据三角形外角性质易得∠BDA′=2∠A;
(2)图②,连结AA′,先根据三角形外角性质得∠BDA′=∠1+∠2,∠CEA=∠3+∠4,则∠BDA′+∠CEA=∠A+∠A′,所以∠BDA′+∠CEA′=2∠A;
(3)理由如下:图③,由折叠性质得∠A′=∠A,∠DEA′=∠DEA,∠A′DE=∠ADE,再根据三角形内角和得(∠A′+∠A)+(∠DEA′+∠DEA)+(∠A′DE+∠ADE)=360°,接着利用平角定理得到2∠A+(180°+∠CEA′)+(180°-∠BDA′)=360°,然后整理得到∠BDA′-∠CEA′=2∠A;
(4)先由折叠性质得∠A′EF=∠AEF,∠B′FE=∠BFE,然后根据平角定义和四边形内角和得到∠1+∠2=180°-(∠A′EF+∠AEF)+180°-(∠B′FE+∠BFE)=2(∠A+∠B)-360°.
解答 解:(1)∠BDA′=2∠A,
理由:∵△ABC沿直线DE折叠,使A点落在CE上,图①,
∴∠A=∠AA′D,
∴∠BDA′=∠A+∠AA′D=2∠A;
故答案为:∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:图②, 连结AA′,
连结AA′,
∵∠BDA′=∠1+∠2,∠CEA=∠3+∠4,
∴∠BDA′+∠CEA=∠1+∠3+∠2+∠4=∠A+∠A′,
而∠A=∠AA′D,
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′-∠CEA′=2∠A.
理由如下:图③,
由翻折可得:∠A′=∠A,∠DEA′=∠DEA,∠A′DE=∠ADE,
由内角和性质得:(∠A′+∠A)+(∠DEA′+∠DEA)+(∠A′DE+∠ADE)=360°,
∴2∠A+(180°+∠CEA′)+(180°-∠BDA′)=360°
∴2∠A+∠CEA′-∠BDA′=0,
∴∠BDA′-∠CEA′=2∠A;
(4)由折叠性质得∠A′EF=∠AEF,∠B′FE=∠BFE,
∴∠1+∠2=180°-(∠A′EF+∠AEF)+180°-(∠B′FE+∠BFE)
=180°-2∠AEF+180°-2∠BFE
=360°-2(360°-∠A-∠B)
=2(∠A+∠B)-360°.
故答案为∠1+∠2=2(∠A+∠B)-360°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.也考查了折叠的性质、三角形外角性质.


科目:初中数学 来源: 题型:解答题
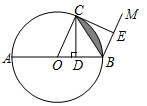 如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.
如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A校 | B校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | 20 | 0.15 | 10 | 0.15 |
| 乙地 | 15 | 0.20 | 20 | 0.20 |

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形ABCD中,E、F分别在AD、DC上,∠ABE=∠CBF=15°,G是AD上另一点,且∠BGD=120°,连接EF、BG、FG、EF、BG交于点H,则下面结论:①DE=DF;②△BEF是等边三角形;③∠BGF=45°;④BG=EG+FG中,正确的是①②④(请填番号)
正方形ABCD中,E、F分别在AD、DC上,∠ABE=∠CBF=15°,G是AD上另一点,且∠BGD=120°,连接EF、BG、FG、EF、BG交于点H,则下面结论:①DE=DF;②△BEF是等边三角形;③∠BGF=45°;④BG=EG+FG中,正确的是①②④(请填番号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
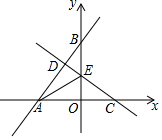 如图,直线l1:y=$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:y=-$\frac{3}{4}$x+b经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
如图,直线l1:y=$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:y=-$\frac{3}{4}$x+b经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若AC+BD=22cm,△OAB的周长是16cm,则EF的长为2.5cm.
如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若AC+BD=22cm,△OAB的周长是16cm,则EF的长为2.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com