
【题目】a![]() b是新规定的一种运算法则:a
b是新规定的一种运算法则:a![]() b=a2+ab,例如3
b=a2+ab,例如3![]() (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.
(1)求(﹣3)![]() 5的值;
5的值;
(2)若(﹣2)![]() x=6,求x的值;
x=6,求x的值;
(3)若3![]() (2
(2![]() x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值.
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.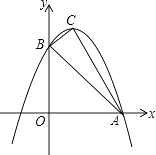
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的妙点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的妙点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的妙点,但点D是(B,A)的妙点.
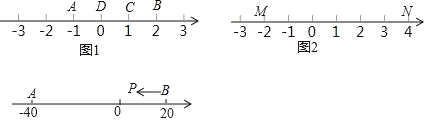
知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
(1)数 所表示的点是(M,N)的妙点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发向左运动,到达点A停止.P点运动多少个单位时,P、A和B中恰有一个点为其余两点的妙点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.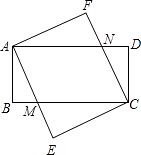
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第6个小房子用的石子数量为 ( )

A. 87 B. 77 C. 70 D. 60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民网为了解百姓对时事政治关心程度,特对18~35岁的青年人每天发微博数量进行调查,设一个人的“日均发微博条数”为m,规定:当m≥10时为甲级,当5≤m<10时为乙级,当0≤m<5时为丙级,现随机抽取20个符合年龄条件的青年人开展调查,所抽青年人的“日均发微博条数”的数据如下:
0 | 8 | 2 | 8 | 10 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)样本数据中为甲级的频率为;(直接填空)
(2)求样本中乙级数据的中位数和众数.
(3)从样本数据为丙级的人中随机抽取2人,用列举法或树状图求抽得2个人的“日均发微博条数”都是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市进行促销活动,甲超市采用“买100减50”的促销方式,即购买商品的总金额满100元但不足200元,少付50元;满200元但不足300元,少付100元;….乙超市采用“打6折”的促销方式,即顾客购买商品的总金额打6折.
(1)若顾客在甲商场购买商品的总金额为x(100≤x<200)元,优惠后得到商家的优惠率为p(p= ![]() ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(2)王强同学认为:如果顾客购买商品的总金额超过100元,实际上甲超市采用“打5折”、乙超市采用“打6折”,那么当然选择甲超市购物.请你举例反驳;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(300≤x<400)元,认为选择哪家商场购买商品花钱较少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com