
【题目】如图,P为⊙O直径AB延长线上的一点,PC切⊙O于点C,过点B作CP的垂线BH交⊙O于点D,连结AC,CD.
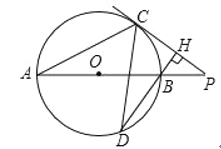
(1)求证:∠PBH=2∠HDC;
(2)若sin∠P=![]() ,BH=3,求BD的长.
,BH=3,求BD的长.
【答案】(1)详见解析;(2)18
【解析】
(1)连接OC,因为PC切⊙O于点C,则OC⊥PC,因为过点B作CP的垂线BH交⊙O于点D,可得DH∥OC,进而得出∠PBH=∠BOC=2∠HDC;
(2)作OM⊥DH于H,设⊙O的半径为r,可得四边形OMHC为矩形,因为sin∠P=![]() ,BH=3,所以BP=4,由△PHB∽△PCO,得
,BH=3,所以BP=4,由△PHB∽△PCO,得![]() ,求得r=12,可得出MH的长,从而求出BD的长.
,求得r=12,可得出MH的长,从而求出BD的长.
解:(1)如图,连接OC,
∵PC切⊙O于点C,
∴OC⊥PC,
∵过点B作CP的垂线BH交⊙O于点D,
∴DH∥OC,
∴∠PBH=∠BOC,
∵∠BOC=2∠HDC,
∴∠PBH=2∠HDC;
(2)如图,作OM⊥DH于H,设⊙O的半径为r,
∵∠OCH=∠OMH=∠CHM=90°,
∴四边形OMHC为矩形,
∵sin∠P=![]() ,BH=3,
,BH=3,
∴![]() ,
,
∴BP=4,
∵OC∥DH,
∴△PHB∽△PCO,
∴![]() ,
,
∴![]() ,解得r=12,
,解得r=12,
∴MH=OC=12,
∴MB=MH﹣BH=12﹣3=9,
∴BD=2MB=18.



科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
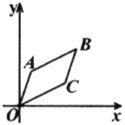
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,若将
,若将![]() 先沿
先沿![]() 轴进行第一次对称变换,所得图形沿
轴进行第一次对称变换,所得图形沿![]() 轴进行第二次对称变换,轴对称变换的对称轴遵循
轴进行第二次对称变换,轴对称变换的对称轴遵循![]() 轴、
轴、![]() 轴、
轴、![]() 轴、
轴、![]() 轴…的规律进行,则经过第2018次变换后,
轴…的规律进行,则经过第2018次变换后,![]() 顶点
顶点![]() 坐标为()
坐标为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
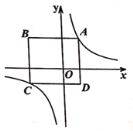
【题目】如图是反比例函数![]() 的图象,点
的图象,点![]() ,
,![]() 分别在图象的两支上,以
分别在图象的两支上,以![]() 为对角线作矩形
为对角线作矩形![]() 且
且![]() 轴.
轴.
(1)当线段![]() 过原点时,分别写出
过原点时,分别写出![]() 与
与![]() ,
,![]() 与
与![]() 的一个等量关系式;
的一个等量关系式;
(2)当![]() 、
、![]() 两点在直线
两点在直线![]() 上时,求矩形
上时,求矩形![]() 的周长;
的周长;
(3)当![]() 时,探究
时,探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
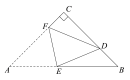
【题目】如图,在△ABC中,AC=BC=4![]() ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,AB=2CD.动点P从点A出发,在四边形ABCD的边上沿A→B→C的方向以1cm/s的速度匀速移动,到达点C时停止移动。已知△APD的面积S(cm 2)与点P运动的时间t(s)之间的函数图象如图②所示,根据题意解答下列问题
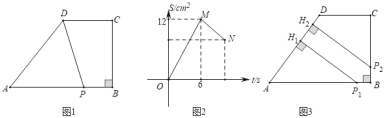
(1)在图①中,AB= cm, BC= cm.
(2)求图2中线段MN的函数关系式(并写出t的取值范围) .
(3)如图③,设动点P用了t1 (s)到达点P1处,用了t2 (s)到达点P2处,分别过P1、P2作AD的垂线,垂足为H1、H2.当P1H1= P2H2=4时,连P1P2,求△BP1P2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
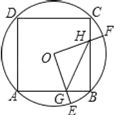
【题目】如图,边长为2的正方形ABCD内接于⊙O,点E是![]() 上一点(不与A、B重合),点F是
上一点(不与A、B重合),点F是![]() 上一点,连接OE,OF,分别与AB,BC交于点G,B,且∠EOF=90°.有下列结论:①
上一点,连接OE,OF,分别与AB,BC交于点G,B,且∠EOF=90°.有下列结论:①![]() =
=![]() ;②四边形OGBH的面积随着点E位置的变化而变化;③△GBH周长的最小值为2+
;②四边形OGBH的面积随着点E位置的变化而变化;③△GBH周长的最小值为2+![]() ;④若BG=1﹣
;④若BG=1﹣![]() ,则BG,GE,
,则BG,GE,![]() 围成的面积是
围成的面积是![]() ,其中正确的是_____.(把所有正确结论的序号都填上)
,其中正确的是_____.(把所有正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com