
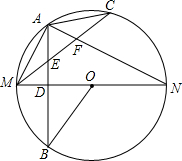
 ��ͼ��ʾ��MN�ǡ�O��ֱ������AB��MN������Ϊ��D������AM��AN����CΪ��AN��һ�㣬��$\widehat{AC}$=$\widehat{AM}$������CM����AB�ڵ�E����AN�ڵ�F���ָ������½��ۣ���MD=DO����$\widehat{AM}$=$\widehat{BM}$���ۡ�ACM+��ANM=��MOB����AE=$\frac{1}{2}$MF��������ȷ�Ľ����Тڢۢܣ������������ȷ���۵���Ŷ����ں����ϣ�
��ͼ��ʾ��MN�ǡ�O��ֱ������AB��MN������Ϊ��D������AM��AN����CΪ��AN��һ�㣬��$\widehat{AC}$=$\widehat{AM}$������CM����AB�ڵ�E����AN�ڵ�F���ָ������½��ۣ���MD=DO����$\widehat{AM}$=$\widehat{BM}$���ۡ�ACM+��ANM=��MOB����AE=$\frac{1}{2}$MF��������ȷ�Ľ����Тڢۢܣ������������ȷ���۵���Ŷ����ں����ϣ� ���� ����AB��MN���ɴ��������ó�����ȷ���ó�$\widehat{AC}=\widehat{AM}=\widehat{BM}$����Բ�ܽǶ�����ֱ�������ε����ʵó��ۢ���ȷ��û�������ó�MD=DO���ٲ�һ����ȷ�����ɵó����ۣ�
��� �⣺��MN�ǡ�O��ֱ����AB��MN��
���MAN=90�㣬$\widehat{AM}$=$\widehat{BM}$��
�ʢ���ȷ��
��$\widehat{AC}$=$\widehat{AM}$��
��$\widehat{AC}=\widehat{AM}=\widehat{BM}$��
���ACM+��ANM=��MOB��
�ʢ���ȷ��
�ߡ�MAE=��AME��
��AE=ME����EAF=��AFM��
��AE=EF��
��AE=$\frac{1}{2}$MF��
�ʢ���ȷ��
û�������ó�MD=DO���ٲ�һ����ȷ��
�ʴ�Ϊ���ڢۢܣ�
���� ���⿼����Բ�ܽǶ����������������Լ�ֱ��������б���ϵ����ߵ���б�ߵ�һ���֪ʶ����������Բ�ܽǶ����ʹ��������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
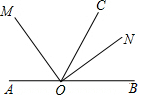 ��ͼ����O��ֱ��AB��һ�㣬OMƽ�֡�AOC��ONƽ�֡�BOC��
��ͼ����O��ֱ��AB��һ�㣬OMƽ�֡�AOC��ONƽ�֡�BOC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������Գ�ͼ�Σ�����ƽ���߾������ĶԳ��� | |
| B�� | ���������ε��ڽ�ƽ���ߣ����ߺ����ߺ�һ | |
| C�� | ֱ�������β�����Գ�ͼ�� | |
| D�� | �ȱ��������������Գ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
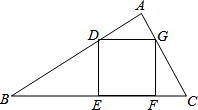 �ڡ�ABC�У�������DEFG����������E��F��BC���ϣ�����������D��G�ֱ���AB��AC�ϣ���ADG�͡�CFG�������Ϊ1����BDE�����Ϊ3����������DEFG�������
�ڡ�ABC�У�������DEFG����������E��F��BC���ϣ�����������D��G�ֱ���AB��AC�ϣ���ADG�͡�CFG�������Ϊ1����BDE�����Ϊ3����������DEFG��������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com