Question

12．如图1，正方形ABCD（四条边相等，四个角是直角）的边长为7cm，点M在边DC上，且CM=2cm，过点M作 ME⊥DC，交BD于点E．，动点P从点D出发沿DC边向M点运动，速度为每秒2cm，当动点P到达M点时，运动停止．连接EP，EC．在此过程中，设P点运动时间为t秒．
（1）EM=5cm，
PC=7-2tcm（用含t的代数式表示），
当t=$\frac{1}{2}$秒时，△EPC的面积为15？
（2）将△EPC沿CP翻折后如图2，点E的对应点为F点，若PF∥EC，则△EPC为等腰三角形，请说明理由并求此时t为何值．
（3）是否存在某一时刻，使得P点到A点、E点的距离之和最短？如果存在，直接写出PA+PE的最小值，如果不存在，请说明理由．

Answer 1

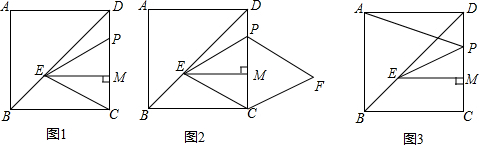
分析 （1）根据平行线分线段成比例定理即可求得EM；根据题意求得PD，进而即可求得PC；根据S_△EPC=$\frac{1}{2}$PC•EM=15即可求得t的值；
（2）根据对折的性质得出PF=PE，∠FPC=∠EPC，由PF∥EC，得出∠FPC=∠PCE，进一步求得∠EPC=∠PCE，根据等角对等边求得PE=CE，证得△EPC为等腰三角形，根据等腰三角形三线合一的性质得出CM=PM=2，即可求得DP=3，从而求得t=$\frac{3}{2}$；
（3）根据轴对称的性质和两点之间线段最短，确定出P点所处的位置，然后根据勾股定理求得即可．

解答 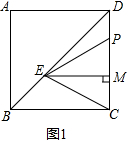解：（1）如图1，∵四边形ABCD是正方形，边长为7cm，
∴BC=DC=7cm，BC⊥DC，
∵ME⊥DC，MC=2，
∴EM∥BC，DM=7-2=5cm，
∴$\frac{EM}{BC}$=$\frac{DM}{DC}$，即$\frac{EM}{7}$=$\frac{5}{7}$，
∴EM=5，
∵DP=2t，
∴PC=7-2t，
∵S_△EPC=$\frac{1}{2}$PC•EM=15，
∴$\frac{1}{2}$（7-2t）×5=15，
解得t=$\frac{1}{2}$；
故答案为5，7-2t，$\frac{1}{2}$．
故答案为：等腰．
（2）△EPC为等腰三角形，
理由：∵△PFC由△PEC反折而成，如图2，
∴PF=PE，∠FPC=∠EPC，
∵PF∥EC，
∴∠FPC=∠PCE，
∴∠EPC=∠PCE，
∴PE=CE，△EPC为等腰三角形，
∵EM⊥DC，
∴CM=PM=2，
∴DP=3，
∴t=$\frac{3}{2}$；
（3）如图3，作A点关于直线CD的对称点F，则DF=AD=7，连接EF，交DC于P，此时PA+PE=PF+PE=EF，EF的长就是PA+PE的最小值；过F点作FN∥CD，交EM的延长线于N，
∵EM⊥CD，AD⊥DC，
∴EN⊥FN，DF⊥FN，
∴四边形DMNF是矩形，
∴MN=DF=7，FN=DM=5，
在RT△ENF中，EN=EM+MN=5+7=12，FN=5，
则EF=$\sqrt{E{N}^{2}+F{N}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13（cm）．
∴PA+PE的最小值为13cm．

点评 本题是四边形的综合题，考查了正方形的性质，平行线分线段成比例定理的应用，等腰三角形的判定和性质，轴对称-最短路线问题，勾股定理的应用等，熟练掌握和运用这些性质定理是解题的关键．