
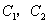 关于
关于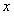 轴对称;抛物线
轴对称;抛物线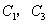 关于y轴对称。抛物线
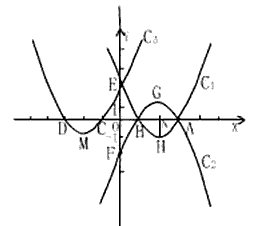
关于y轴对称。抛物线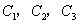 与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线
与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线 的顶点。HN垂直于x轴,垂足为N,且
的顶点。HN垂直于x轴,垂足为N,且 
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:044
已知:如图,抛物线![]() 关于
关于![]() 轴对称;抛物线
轴对称;抛物线![]() 关于y轴对称。抛物线
关于y轴对称。抛物线![]() 与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线
与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线![]() 的顶点。HN垂直于x轴,垂足为N,且
的顶点。HN垂直于x轴,垂足为N,且![]()
(1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形 ;等腰梯形 ;平行四边形 ;梯形 ;(每种特殊四边形只能写一个,写错、多写记0分)
(2)证明其中任意一个特殊四边形;
(3)写出你证明的特殊四边形的性质。

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,抛物线与
轴交于点
,与
轴交于
、
两点,点
的坐标为
.
(1)求抛物线的解析式及顶点的坐标;
(2)设点是在第一象限内抛物线上的一个动点,求使与四边形
面积相等的四边形
的点
的坐标;
(3)求的面积.
查看答案和解析>>
科目:初中数学 来源:2012届上海市闵行区初三二模数学试卷(带解析) 题型:解答题
已知:如图,抛物线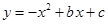 与
与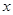 轴的负半轴相交于点
轴的负半轴相交于点 ,与
,与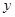 轴相交于点
轴相交于点 (0,3),且∠
(0,3),且∠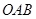 的余切值为
的余切值为 .
.
(1)求该抛物线的表达式,并写出顶点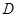 的坐标;
的坐标;
(2)设该抛物线的对称轴为直线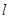 ,点
,点 关于直线
关于直线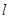 的对称点为
的对称点为 ,
,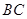 与直线
与直线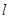 相交于点
相交于点 .点
.点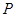 在直线
在直线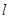 上,如果点
上,如果点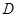 是△
是△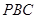 的重心,求点
的重心,求点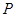 的坐标;
的坐标;
(3)在(2)的条件下,将(1)所求得的抛物线沿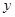 轴向上或向下平移后顶点为点
轴向上或向下平移后顶点为点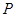 ,写出平移后抛物线的表达式.点
,写出平移后抛物线的表达式.点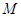 在平移后的抛物线上,且△
在平移后的抛物线上,且△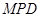 的面积等于△
的面积等于△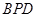 的面积的2倍,求点
的面积的2倍,求点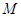 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市闵行区初三二模数学试卷(解析版) 题型:解答题
已知:如图,抛物线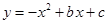 与
与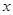 轴的负半轴相交于点
轴的负半轴相交于点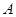 ,与
,与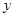 轴相交于点
轴相交于点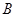 (0,3),且∠
(0,3),且∠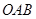 的余切值为
的余切值为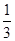 .
.
(1)求该抛物线的表达式,并写出顶点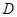 的坐标;
的坐标;
(2)设该抛物线的对称轴为直线 ,点
,点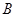 关于直线
关于直线 的对称点为
的对称点为 ,
,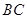 与直线
与直线 相交于点
相交于点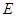 .点
.点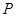 在直线
在直线 上,如果点
上,如果点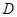 是△
是△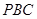 的重心,求点
的重心,求点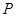 的坐标;
的坐标;
(3)在(2)的条件下,将(1)所求得的抛物线沿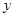 轴向上或向下平移后顶点为点
轴向上或向下平移后顶点为点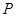 ,写出平移后抛物线的表达式.点
,写出平移后抛物线的表达式.点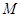 在平移后的抛物线上,且△
在平移后的抛物线上,且△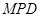 的面积等于△
的面积等于△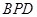 的面积的2倍,求点
的面积的2倍,求点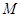 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com