
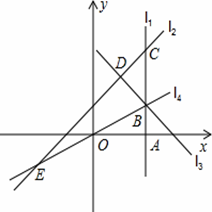
如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l 2于点E.当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.
(1)若点B在线段AC上,且S1![]() =S2,则B点坐标为 ;
=S2,则B点坐标为 ;
(2)若点B在直线l1上,且S2=![]() S1,则∠BOA的度数为 .
S1,则∠BOA的度数为 .
(1)(2,0);(2)15°或75°。
【解析】(1)设B的坐标是(2,m),则△BCD是等腰直角三角形。
∵![]() ,∴
,∴![]() 。
。
∴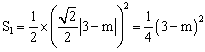 。
。
设直线l4的解析式是y=kx,则2k=m,解得:![]() 。
。
∴直线l4的解析式是![]() 。
。
根据题意得: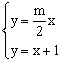 ,解得:
,解得: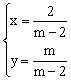 。
。
∴E的坐标是(![]() ,
,![]() )。
)。
∴![]() 。
。
∴![]() 。
。
当S1=S2时,![]() 。
。
解得:m=0,m=4(不在线段AC上,舍去),m=3(l2和l4重合,舍去)。
∴B的坐标是(2,0)。
(2)分三种情况:
①当点B在线段AC上时(如图1),
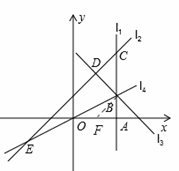
由S2=![]() S 1得:
S 1得:![]() 。
。
解得:![]() 或
或![]() (不在线段AC上,舍去),或m=3(l2和l4重合,舍去)。
(不在线段AC上,舍去),或m=3(l2和l4重合,舍去)。
∴AB=![]() 。
。
在OA上取点F,使OF=BF,连接BF,设OF=BF=x,
则AF=2-x,根据勾股定理,得![]() ,解得
,解得![]() 。
。
∴sin∠BFA=![]() 。∴∠BFA=30°。∴∠BOA=15°。
。∴∠BFA=30°。∴∠BOA=15°。
②当点B在AC延长线上时(如图2),
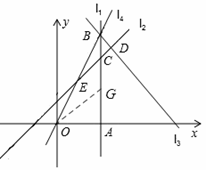
此时,![]() ,
,
由S2=![]() S 1得:
S 1得:![]() 。
。
解得:![]() 或
或![]() (不在AC延长线上,舍去),或m=3(l2和l4重合,舍去)。
(不在AC延长线上,舍去),或m=3(l2和l4重合,舍去)。
∴AB=![]() 。
。
在AB上取点G,使BG=OG,连接OG,设BG=OG=x,
则AG=![]() ,根据勾股定理,得
,根据勾股定理,得![]() ,解得
,解得![]()
∴sin∠OGA=![]() 。∴∠OGA =30°。∴∠OBA=15°。∴∠BOA=75°。
。∴∠OGA =30°。∴∠OBA=15°。∴∠BOA=75°。
③当点B在CA延长线上时(如图3),
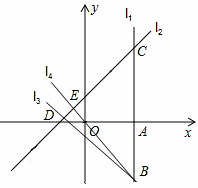
此时,![]() ,
,
由S2=![]() S 1得:
S 1得:![]() 。
。
解得: m=3(l2和l4重合,舍去)。
∴此时满足条件的点B不存在。
综上所述,∠BOA的度数为15°或75°。


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
 (2012•宁波模拟)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S1=
(2012•宁波模拟)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S1=| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012=
(2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012=查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•义乌市)如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.
(2013•义乌市)如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
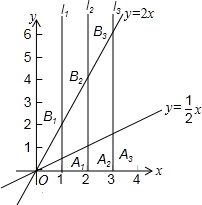 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年浙江省义乌市中考数学试卷(解析版) 题型:填空题
 S1,则∠BOA的度数为 .
S1,则∠BOA的度数为 .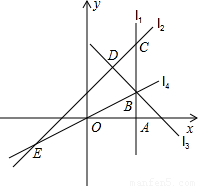
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com