
分析 可设每件羽绒服应降价x元,因为每件羽绒服降阶1元,平均每天可多售出2件,所以降价后每件可盈利(40-x)元,每天可售(20+2x)件,又因平均每天要盈利1200元,所以可列方程(40-x)(20+2x)=1200,即可求解.
解答 解:设每件羽绒服应降价x元,
依题意得:(40-x)(20+2x)=1200,
整理得:x2-30x+200=0,
解得:x1=10;x2=20.
当x1=10时,20+2x=20+20=40,
或当x2=20时,20+2x=20+40=60.
答:每件羽绒服应降价10元,此时的销售量是40件,或每件羽绒服应降价20元,此时的销售量是60件.
点评 考查了一元二次方程的应用,得到现在的销售量是解决本题的难点;根据每天盈利得到相应的等量关系是解决本题的关键.


科目:初中数学 来源: 题型:解答题
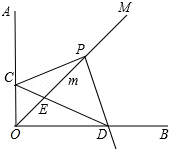 已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.
已知∠AOB=90°,OM是∠AOB的平分线,将一个直角三角板的直角顶点P放在射线OM上,OP=2,移动直角三角板,两边分别交射线OA,OB与点C,D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+50x-1400=0 | B. | x2-65x-250=0 | C. | x2-30x-1400=0 | D. | x2+50x-250=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
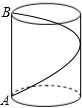 如图,有一圆柱油罐,已知油罐的底面圆的周长是12米,高是5米,要从点A起环绕油罐建梯子,梯子的顶端正好到达点A的正上方点B,则梯子最短需多长?
如图,有一圆柱油罐,已知油罐的底面圆的周长是12米,高是5米,要从点A起环绕油罐建梯子,梯子的顶端正好到达点A的正上方点B,则梯子最短需多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
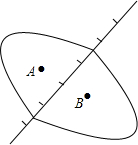 如图是王先生祖居的位置图,由于保存不慎已残缺不全,但可知钟楼的坐标为A(5,-2),街口坐标为B(5,2),资料记载王先生祖居的老屋坐标为(1,1),你能帮王先生找到祖居的老屋吗?
如图是王先生祖居的位置图,由于保存不慎已残缺不全,但可知钟楼的坐标为A(5,-2),街口坐标为B(5,2),资料记载王先生祖居的老屋坐标为(1,1),你能帮王先生找到祖居的老屋吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com