
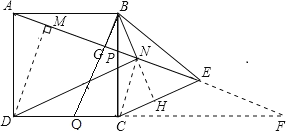
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.

【答案】![]()
【解析】分析:首先得出∠AGB=90°,过点D作DM⊥AN于M,根据五点共圆的性质得出Rt△DMN,Rt△BGN都是等腰直角三角形,然后根据DN的长度得出正方形的边长,根据△ABP的等积法得出BG的长度,然后根据△BGP和△CNP相似得出CN的长度,最后根据等腰直角三角形的性质得出CE的长度.
详解:∵BP=CQ,则△ABP≌△BCQ,∴∠AGB=90°,
连接CN,延长BN交CE于H. 过点D作DM⊥AN于M,
∴Rt△ADM≌Rt△ABG,DM=AG, ∵BN平分∠CBE,∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN, ∴△BCN≌△BEN,
∴CN=NE,△CEN是等腰三角形,
延长AE交DC延长线于F,则有:∠BAG=∠BEG=∠CFE=∠BCN,
A,B,C,D,N五点共圆,∠AND=∠BNG=45°[AB弦所对圆周角=45°]
Rt△DMN,Rt△BGN都是等腰直角三角形,
∵DN=![]() , ∴AB=MN=
, ∴AB=MN=![]() ,根据△ABP的等积法可得:BG=
,根据△ABP的等积法可得:BG=![]() ,
,
∵△BGP∽△CNP,则CN=2BG=![]() ,则CE=
,则CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E. 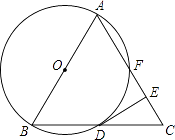
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号中:8,﹣![]() ,+2.8,π,
,+2.8,π,![]() ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……
正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A,B两点,且点A的横坐标为4,
(k>0)交于A,B两点,且点A的横坐标为4,
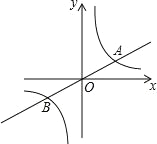
(1)求 k的值;
(2)利用图形直接写出不等式![]() x>
x>![]() 的解;
的解;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
(k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①由4根火柴棍围成;图②由12根火柴棍围成;图③由24根火柴棍围成;…按此规律,则第⑥个图形由( )根火柴棍围成.

A. 60 B. 72 C. 84 D. 112
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是APQM面积的 ![]() 时,求APQM面积.
时,求APQM面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1 , 连接AD1、BC1 . 若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:
①△A1AD1≌△CC1B;
②当x=1时,四边形ABC1D1是菱形;
③当x=2时,△BDD1为等边三角形;
④S= ![]() (x﹣2)2(0≤x≤2).
(x﹣2)2(0≤x≤2).
其中正确的是(将所有正确答案的序号都填写在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com