
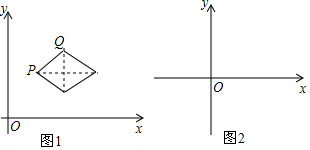
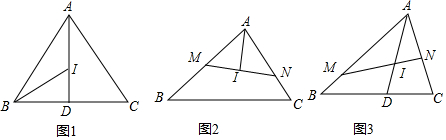
分析 (1)如图1中,观察图象可知:R、S能够成为点A,B的“相关菱形”顶点.
(2)如图2中,过点A作AH垂直x轴于H点.根据正方形的性质可知BH=4,由此即可解决问题.
(3)根据正方形的性质,画出图象,即可判断.
解答 解:(1)如图1中,观察图象可知:R、S能够成为点A,B的“相关菱形”顶点.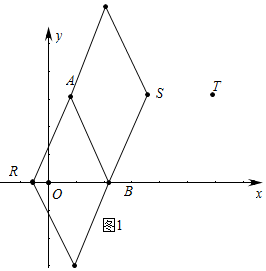
故答案为R,S.
(2)如图2中,过点A作AH垂直x轴于H点.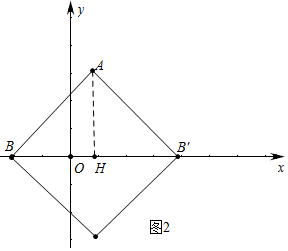
∵点A,B的“相关菱形”为正方形,
∴△ABH为等腰直角三角形.
∵A(1,4),
∴BH=AH=4.
∴b=-3或5.
(3)如图3中,观察图象可知,满足条件的b的范围为:-5≤b≤0或3≤b≤8.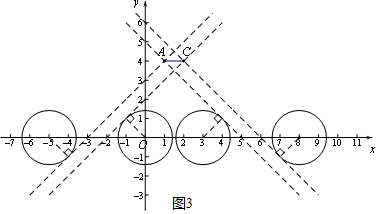
点评 本题考查圆综合题、菱形的性质、正方形的性质、点P,Q的“相关菱形”的定义等知识,解题的关键是理解题意,学会利用图象解决问题,学会用分类讨论的思想思考问题,注意一题多解,属于中考创新题目.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
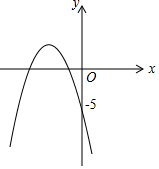 已知抛物线y=ax2+x+b上的一点为(-1,-7),与y轴交点为(0,-5)
已知抛物线y=ax2+x+b上的一点为(-1,-7),与y轴交点为(0,-5)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 【问题情境】
【问题情境】| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | m | … |
| y | … | 4$\frac{1}{4}$ | 3$\frac{1}{3}$ | 2$\frac{1}{2}$ | 2 | 2$\frac{1}{2}$ | 3$\frac{1}{3}$ | 4$\frac{1}{4}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:
阅读下面材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
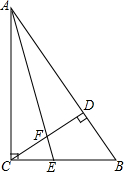 已知:如图,在△ABC中,∠ACB=90°,AE是∠BAC的角平分线,CD是高,AE与CD相交于点F.
已知:如图,在△ABC中,∠ACB=90°,AE是∠BAC的角平分线,CD是高,AE与CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 8 | 6 | 4 | 2 | 0 | … |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com