
分析 (1)根据整式的混合运算计算即可;
(2)根据分式的混合运算计算即可.
解答 (1)解:
原式=${a}^{2}-ab-2{b}^{2}+{a}^{3}b+2{b}^{2}-4{a}^{2}×\frac{1}{4}ab$,
=a2-ab+a3b-a3b,
=a2-ab;
(2)解:
原式=$\frac{1}{x}÷[\frac{{x}^{2}+1}{x(x-1)}-\frac{2x}{x(x-1)}]$,
=$\frac{1}{x}÷\frac{{x}^{2}+1-2x}{x(x-1)}$,
=$\frac{1}{x}÷\frac{(x-1)^{2}}{x(x-1)}$,
=$\frac{1}{x}×\frac{x}{x-1}$,
=$\frac{1}{x-1}$.
点评 此题考查整式和分式混合计算,关键是根据混合计算的顺序进行计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
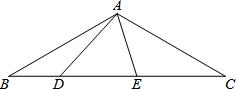 如图,在△ABC中,AB=AC,∠BAC=120°,D、E为BC边上的点,且∠DAE=60°.
如图,在△ABC中,AB=AC,∠BAC=120°,D、E为BC边上的点,且∠DAE=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| S2 | 1 | 1 | 1.2 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | |
| 甲队 | 177 | 176 | 175 | 172 | 175 |
| 乙队 | 170 | 175 | 173 | 174 | 183 |
| A. | $\overline{x}$甲=$\overline{x}$乙,S2甲>S2乙 | B. | $\overline{x}$甲<$\overline{x}$乙,S2甲<S2乙 | ||
| C. | $\overline{x}$甲>$\overline{x}$乙,S2甲>S2乙 | D. | $\overline{x}$甲=$\overline{x}$乙,S2甲<S2乙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com