
 �����γ�����ȵĺ����ھ����ֱ��ס����������̶�ͬʱ�����ھ���ͼ�Ƿ�ӳ���ں�������y���ף����ھ�ʱ��x��ʱ��֮���ϵ�IJ���ͼ�������������⣺
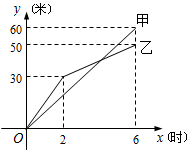
�����γ�����ȵĺ����ھ����ֱ��ס����������̶�ͬʱ�����ھ���ͼ�Ƿ�ӳ���ں�������y���ף����ھ�ʱ��x��ʱ��֮���ϵ�IJ���ͼ�������������⣺���� ��1����ͼ�ɵý��ۣ�
��2�����ֱ��OC�Ľ���ʽ���ɣ�
��3������ͬʱ��������Կ��ɴ����е������⣮
��� �⣺��1����ͼ��֪���Ҷӿ��ڵ�30��ʱ������2Сʱ��
����6Сʱʱ��������60�ף��Ҷ�����50�ף�
���Լӱ��ҶӶ�����60-50=10�ף�
�ʴ�Ϊ��2��10��
��2����ֱ��OC�Ľ���ʽΪ��y=kx��k��0����
��C��6��60������ã�6k=60��
k=10��
��ֱ��OC�Ľ���ʽΪ��y=10x��
��y��x֮��ĺ�����ϵʽ�ǣ�y=10x��0��x��6����
�ʴ��ǣ�y=10x��0��x��6����
��3����ӦÿСʱ����xǧ�ף��������ͬʱ���110���ھ�����
$\frac{110-60}{10}$=$\frac{110-50}{x+5}$��
��ã�x=7��
�����飺x=7��ԭ���̵ĸ���
��x+5=12��
���Ҷ��ڿ���6Сʱ��ʩ���ٶ�ӦΪÿСʱ 12�ף��������ͬʱ���110���ھ�����
�ʴ��ǣ�12��
���� ������һ�κ�����Ӧ�ã����������ô���ϵ������һ�κ����Ľ���ʽ�����˺����뷽�����ϵ�˼�룻����Ĺؼ�������ס����������̶���ͼ��������ʾ��ͼ������壮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
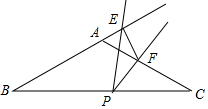 ��ͼ���ڵ�����ABC�У�AB=AC=8����BAC=120�㣬PΪBC���е㣬С�۰Ѻ�30��ǵ������ǰ��30��ǵĶ�����ڵ�P����P����ת�����ǰ�����߷ֱ�BA���ӳ��ߺͱ�AC�ڵ�E��F��
��ͼ���ڵ�����ABC�У�AB=AC=8����BAC=120�㣬PΪBC���е㣬С�۰Ѻ�30��ǵ������ǰ��30��ǵĶ�����ڵ�P����P����ת�����ǰ�����߷ֱ�BA���ӳ��ߺͱ�AC�ڵ�E��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-3 | B�� | x��0 | C�� | x��3 | D�� | -3��x��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com