
【题目】如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB= ![]() ,则此三角形移动的距离AA′是( )
,则此三角形移动的距离AA′是( ) 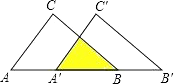
A.![]() ﹣1
﹣1
B.![]()
C.1
D.![]()
【答案】A
【解析】解:设BC与A′C′交于点E, 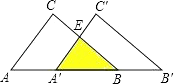
由平移的性质知,AC∥A′C′
∴△BEA′∽△BCA
∴S△BEA′:S△BCA=A′B2:AB2=1:2
∵AB= ![]()
∴A′B=1
∴AA′=AB﹣A′B= ![]() ﹣1
﹣1
故选A.
【考点精析】关于本题考查的平移的性质和相似三角形的判定与性质,需要了解①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中, 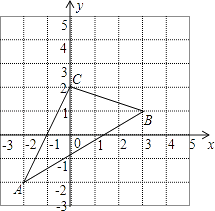
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF. 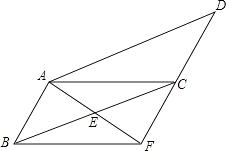
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
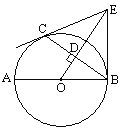
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
(1)求证:BE与⊙O相切;
(2)连结AD并延长交BE于点F,若OB=6,且sin∠ABC=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com