
二次函数 的图象如图,则一次函数y=mx+n的图象经过
的图象如图,则一次函数y=mx+n的图象经过
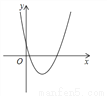
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
C 【解析】试题分析:∵抛物线的顶点(-m,n)在第四象限, ∴-m>0,n<0, ∴m<0, ∴一次函数y=mx+n的图象经过二、三、四象限, 故选C. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:单选题
下列命题中,真命题是( )
A. 有两边相等的平行四边形是菱形 B. 对角线垂直的四边形是菱形
C. 四个角相等的菱形是正方形 D. 两条对角线相等的四边形是矩形
A 【解析】试题分析:A.反例:等腰梯形;B.反例:风筝型;D.反例:等腰梯形 故选C查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
如图,以直角三角形的三边为边,分别向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形有( )

A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】试题分析:(1)S1=,S2=,S3=,∵,∴,∴S1+S2=S3. (2)S1=,S2=,S3=,∵,∴,∴S1+S2=S3. (3)S1=,S2=,S3=,∵,∴,∴S1+S2=S3. (4)S1=,S2=,S3=,∵,∴S1+S2=S3. 综上,可得:面积关系满足S1+S2=S3图形有4个. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:解答题
用适当的方法解下列方程。
(1)3x(x+3)=2(x+3)
(2)2x2?4x?3=0.
(1)x1=?3,x2= (2) 【解析】试题分析:第小题用因式分解法,第小题用公式法. 试题解析::(1)3x(x+3)-2(x+3)=0, (x+3)(3x-2)=0, 或 (2) ∴ ∴x1=1+,x2=1-.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:单选题
已知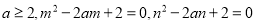 ,则
,则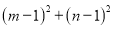 的最小值是( )。
的最小值是( )。
A. 6 B. 3 C. -3 D. 0
A 【解析】试题分析:∵m2-2am+2=0,n2-2an+2=0, ∴m,n是关于x的一元二次方程x2-2ax+2=0的两个根, ∴m+n=2a,mn=2, ∴(m-1)2+(n-1)2=m2-2m+1+n2-2n+1=(m+n)2-2mn-2(m+n)+2=4a2-4-4a+2=4(a-)2-3, ∵a≥2, ∴当a=2时,(m-1)2+(n-1)2有最小值...查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:单选题
把抛物线 先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )。
先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )。
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:解答题
已知y+3与x+2成正比例,且当x=3时,y=7.
(1)写出y与x之间的函数关系式;
(2)当x=﹣1时,求y的值.
(1)y与x之间的函数关系式是y=2x+1;(2)y=﹣1. 【解析】试题分析:(1)根据成正比例关系,利用待定系数法求解即可; (2)把x=-1代入(1)的函数解析式即可求出y的值. 试题解析:(1)设y+3=k(x+2)(k≠0). ∵当x=3时,y=7,∴7+3=k(3+2),解得,k=2. ∴y+3=2x+4∴y与x之间的函数关系式是y=2x+1; (2...查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:单选题
在圆的周长C=2πr中,常量与变量分别是( ).
A. 2是常量,C、π、r是变量 B. 2是常量,C、r是变量
C. C、2是常量,r是变量 D. 2是常量,C、r是变量
B 【解析】在圆的周长公式C=2πr中,C与r是改变的,π是不变的;可得变量是C,r,常量是2π. 故选:B.查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
 有意义的条件是( )
有意义的条件是( )
A. 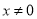 B.
B. 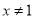 C.
C.  且
且 D.
D.  或
或
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com