Question

19．如图1，共直角边AB的两个直角三角形中，∠ABC=∠BAD=90°，AC交BD于P，且tan∠C=$\frac{AP}{PC}$．
（1）求证：AD=AB；
（2）如图2，BE⊥CD于E交AC于F．
①若F为AC的中点，求$\frac{EC}{DE}$的值；
②当∠BDC=75°时，请直接写出$\frac{EC}{DE}$的值．

Answer 1

分析 （1）根据AD∥BC得$\frac{AP}{PC}$=$\frac{AD}{BC}$，又tan∠C=$\frac{AB}{BC}$故$\frac{AD}{BC}=\frac{AB}{BC}$故AD=AB．
（2）①在图2中，过D作DH⊥BC于H，延长BE交AD延长线于G，易证ABHD为正方形，设其边长为a，DG=b，根据△ABC∽△DGC，得到a、b的关系即可解决问题．
②根据条件推出∠HDC=∠DCG=30°即可解决问题．

解答 解：（1）∵∠DAB+∠ABC=180°，
∴AD∥BC，
∴$\frac{AP}{PC}$=$\frac{AD}{BC}$，
∵tan∠C=$\frac{AB}{BC}$，
∴$\frac{AD}{BC}=\frac{AB}{BC}$，
∴AD=AB．
（2）①在图2中，过D作DH⊥BC于H，延长BE交AD延长线于G，易证ABHD为正方形，设其边长为a，DG=b，
∵AG∥BC，
∴$\frac{AG}{BC}=\frac{AF}{FC}$，
∵AF=FC，
∴AG=BC，
∴四边形ABCG是平行四边形，
∵∠ABC=90°
∴四边形ABCG是矩形，
∴FB=FC，∠BCG=∠AGC=90°，
∴∠FBC=∠FCB，
∵∠FBC+∠BC，E=90°，∠BCE+∠ECG=90°，
∴∠ECG=∠FBC，
∴∠DCG=∠ACB，
∵∠ABC=∠DGC=90°
∴△ABC∽△DGC，
∴$\frac{AB}{DG}=\frac{BC}{CG}$，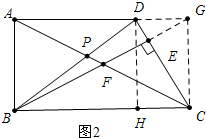
∴$\frac{a}{b}=\frac{a+b}{a}$，
∴a²-ab-b²=0，
∴a=$\frac{1+\sqrt{5}}{2}b$（或a=$\frac{1-\sqrt{5}}{2}b$舍弃），
∵DG∥BC，
∴$\frac{EC}{DE}$=$\frac{BC}{DG}$=$\frac{a+b}{b}$=$\frac{\frac{1+\sqrt{5}}{2}b+b}{b}$=$\frac{3+\sqrt{5}}{2}$，
②由1可知四边形ABHD是正方形，
∵∠BDC=75°，∠BDH=45°，
∴∠HDC=∠DCG=30°，
∵∠DGC=90°，
∴∠CDG=60°，∠DGE=30°，
设CH=m，则DC=2CH=2m，BH=DH=$\sqrt{3}$m
∴EC=$\frac{1}{2}$BC=$\frac{1}{2}$（m+$\sqrt{3}$m），DE=DC-CE=2m-$\frac{1}{2}$（m+$\sqrt{3}$m），
∴$\frac{CE}{DE}$=$\frac{\frac{1}{2}（m+\sqrt{3}m）}{2m-\frac{1}{2}（m+\sqrt{3}m）}$=$\frac{2\sqrt{3}+3}{3}$．

点评 本题考查正方形的判定和性质、相似三角形的判定和性质、勾股定理等知识，添加辅助线构造特殊图形是解决问题的关键．