
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
【答案】3﹣![]()
【解析】试题分析:感知:先利用矩形性质得:∠D=∠C=90°,再利用同角的余角相等得:∠DAE=∠FEC,根据已知边的长度计算出AD=CE=3,则由ASA证得:△ADE≌△ECF;
探究:利用两角相等证明△PDE∽△ECF;
应用:作辅助线,构建如图②一样的相似三角形,利用探究得:△PDE∽△EGF,则 ![]() =
=![]() ,所以
,所以 ![]() =
=![]() ,再利用△PEF的面积是6,列式可得:PEEF=12,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
,再利用△PEF的面积是6,列式可得:PEEF=12,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
试题解析:证明:感知:如图①.∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DAE+∠DEA=90°.∵EF⊥AE,∴∠AEF=90°,∴∠DEA+∠FEC=90°,∴∠DAE=∠FEC.∵DE=1,CD=4,∴CE=3.∵AD=3,∴AD=CE,∴△ADE≌△ECF(ASA);
探究:如图②.∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DPE+∠DEP=90°.∵EF⊥PE,∴∠PEF=90°,∴∠DEP+∠FEC=90°,∴∠DPE=∠FEC,∴△PDE∽△ECF;
应用:如图③,过F作FG⊥DC于G.∵四边形ABCD为矩形,∴AB∥CD,∴FG=BC=3.∵PE⊥EF,∴S△PEF=![]() PEEF=6,∴PEEF=12,同理得:△PDE∽△EGF,∴
PEEF=6,∴PEEF=12,同理得:△PDE∽△EGF,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=3PE,∴3PE2=12,∴PE=±2.∵PE>0,∴PE=2.在Rt△PDE中,由勾股定理得:PD=
,∴EF=3PE,∴3PE2=12,∴PE=±2.∵PE>0,∴PE=2.在Rt△PDE中,由勾股定理得:PD=![]() =
=![]() ,∴AP=AD﹣PD=3﹣
,∴AP=AD﹣PD=3﹣![]() .故答案为:3﹣
.故答案为:3﹣![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商店分两次购进A,B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
A | B | ||
第一次 | 20 | 30 | 2800 |
第二次 | 30 | 20 | 2200 |
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n(m<n)是关于x的方程(x–a)(x–b)=2的两根,若a<b,则下列判断正确的是
A. a<m<b<n B. m<a<n<b
C. a<m<n<d D. m<a<b<n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线。且点B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,试设明:
(1)BD=DE+CE;
(2)若直线AE绕A点旋转到图2位置(BD<CE),其余条件不变时,则BD与DE、CE的关系如何?
(3)若直线AE绕A点旋转到图3位置(CE<BD),其余条件不变时,则BD与DE、CE的关系 。(直接写出结果)



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(﹣1,0),点B(3,0).在第三象限内有一点M(﹣2,m).
(1)请用含m的式子表示△ABM的面积;
(2)当m=-![]() 时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使△BMP的面积与△ABM的面积相等,请求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 的角平分线OC上一点,PN
的角平分线OC上一点,PN![]() OB于点N,点M是线段ON上一点,已知OM=3,ON=4,点D为OA上一点,若满足PD=PM,则OD的长度为________
OB于点N,点M是线段ON上一点,已知OM=3,ON=4,点D为OA上一点,若满足PD=PM,则OD的长度为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
A:自带白开水;B:瓶装矿泉水;C:碳酸饮料;D:非碳酸饮料.
根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:


(1)这个班级有多少名同学?并补全条形统计图.
(2)若该班同学每人每天只饮用一种饮品(每种仅限1瓶,价格如下表),则该班同学用于饮品上的人均花费是多少元?
饮品名称 | 自带白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)若我市约有初中生4万人,估计我市初中生每天用于饮品上的花费是多少元?
(4)为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,请用列表法或树状图法求出恰好抽到2名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )

A.(S.S.S.) B.(S.A.S.) C.(A.S.A.) D.(A.A.S.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.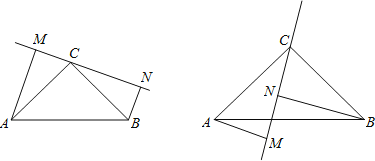
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com