【题目】解方程：
（1）5x﹣6=3x+2；
（2）1﹣3(8﹣x)=﹣2(15﹣2x)；
（3）
1；
（4）
1．
【答案】（1）x=4；（2）x=7；（3）
；（4）
【解析】
（1）移项、合并同类项、系数化1即可；
（2）去括号、移项、合并同类项、系数化1即可；
（3）去分母、去括号、移项、合并同类项、系数化1即可；
（4）去分母、去括号、移项、合并同类项、系数化1即可．
解：（1）5x﹣6=3x+2
移项，得5x﹣3x =6+2
合并同类项，得2x=8
系数化1，得x=4
（2）1﹣3(8﹣x)=﹣2(15﹣2x)
去括号，得1﹣24+3x=-30+4x
移项，得3x-4x =-30+24-1
合并同类项，得-x=-7
系数化1，得x=7
（3）
1
去分母，得
去括号，得
移项，得
合并同类项，得
系数化1，得
（4）
1
去分母，得
去括号，得
移项，得
合并同类项，得
系数化1，得
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，已知反比例函数
的图象与反比例函数
的图象关于
轴对称，
，
是函数图象上的两点，连接
，点
是函数图象上的一点，连接
，
.
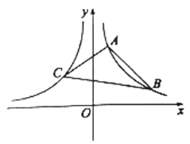
（1）求
，
的值；
（2）求所在直线的表达式；
（3）求
的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.5米，到旗杆的水平距离DC＝20米，求旗杆的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线y=
x+2与x轴交于点A，与y轴交于点C，抛物线y=
x2+bx+c经过A、C两点，与x轴的另一交点为点B．
（1）求抛物线的函数表达式；
（2）点D为直线AC上方抛物线上一动点；
①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1， △BCE的面积为S2， 求
的最大值；
②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，BE∥GF，∠1＝∠3，∠DBC＝70°，求∠EDB的大小．
阅读下面的解答过程，并填空(理由或数学式)
解：∵BE∥GF(已知)
∴∠2＝∠3( )
∵∠1＝∠3( )
∴∠1＝( )( )
∴DE∥( )( )
∴∠EDB+∠DBC＝180°( )
∴∠EDB＝180°﹣∠DBC(等式性质)
∵∠DBC＝( )(已知)
∴∠EDB＝180°﹣70°＝110°
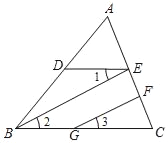
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF．
（1）求证：BF=2AE；
（2）若CD=3
，求AD的长．
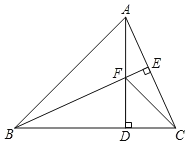
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD⊥BC于D，EG⊥BC于G，∠E=∠1，可得AD平分∠BAC。
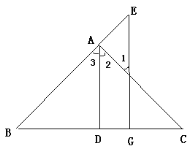
理由如下：
AD⊥BC于D，EG⊥BC于G，（已知）
∠ADC=∠EGC=90°，（ ）
AD‖EG，（ ）
∠1=∠2，（ ）
=∠3，（两直线平行，同位角相等）
又∠E=∠1（已知）
= （等量代换）
AD平分∠BAC（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
