
【题目】如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分B.相等C.互相垂直D.互相垂直平分
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.
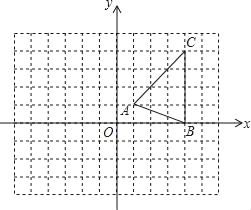
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为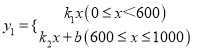 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).
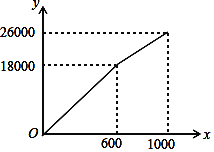
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015德阳)大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年史上最长的寒假结束后,学生复学,某学校为了增强学生体质,鼓励学生在不聚集的情况下加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买![]() 根跳绳和
根跳绳和![]() 个毽子共需
个毽子共需![]() 元;购买
元;购买![]() 根跳绳和
根跳绳和![]() 个毽子共需
个毽子共需![]() 元.
元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是![]() ,且购买的总费用不能超过
,且购买的总费用不能超过![]() 元;若要求购买跳绳的数量多于
元;若要求购买跳绳的数量多于![]() 根,通过计算说明共有哪几种购买跳绳的方案.
根,通过计算说明共有哪几种购买跳绳的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.

(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位的速度运动.点
个单位的速度运动.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位的速度运动,点
个单位的速度运动,点![]() 到达点
到达点![]() 时,
时,![]() 两点同时停止运动.点
两点同时停止运动.点![]() 不与点
不与点![]() 重合时,以为
重合时,以为![]() 邻边作
邻边作![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
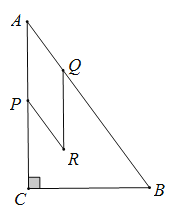
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)当点![]() 在
在![]() 边上时,设
边上时,设![]() 与
与![]() 重叠部分图形面积为
重叠部分图形面积为![]() 求
求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)连结![]() ,当射线
,当射线![]() 平分
平分![]() 面积时,直接写出
面积时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数![]() (人)与时间
(人)与时间![]() (分钟)的变化情况,数据如下表:(表中9-15表示
(分钟)的变化情况,数据如下表:(表中9-15表示![]() )
)
时间 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9~15 |
人数 | 0 | 170 | 320 | 450 | 560 | 650 | 720 | 770 | 800 | 810 | 810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com