
【题目】2018年宜宾市创建全国文明城市的过程中,某小区决定购买文明用语提示牌和文明信息公示栏.若购买2个提示牌和3个公示栏需要510元;购买3个提示牌和5个公示栏需要840元.
(1)求提示牌和公示栏的单价各是多少元?
(2)若该小区购买提示牌和公示栏共50个,要求购买公示栏至少12个,且总费用不超过3200元.请你列举出所有购买方案,并指出哪种方案费用最少,最少费用为多少元?
【答案】(1)提示牌和公示栏的单价各是30元,150元;(2)有三种方案:方案1:购买12个公示栏,38个提示牌;方案2:购买13个公示栏,37个提示牌;方案3:购买14个公示栏,36个提示牌. 当购买12个公示栏,38个提示牌时,费用最少,最少费用为![]() 元.
元.
【解析】
(1)设提示牌和公示栏的单价各是![]() 元,
元,![]() 元,根据“①购买2个提示牌和3个公示栏需要510元;②购买3个提示牌和5个公示栏需要840元”列出方程组,解方程组即可求解;(2)设购买
元,根据“①购买2个提示牌和3个公示栏需要510元;②购买3个提示牌和5个公示栏需要840元”列出方程组,解方程组即可求解;(2)设购买![]() 个公示栏,则购买提示牌(
个公示栏,则购买提示牌(![]() )个,根据“购买公示栏至少12个,且总费用不超过3200元”列出不等式组,解不等式组求m的取值范围,由于m取整数,由此即可确定m的值,从而确定购买方案,再计算最少费用即可.
)个,根据“购买公示栏至少12个,且总费用不超过3200元”列出不等式组,解不等式组求m的取值范围,由于m取整数,由此即可确定m的值,从而确定购买方案,再计算最少费用即可.
(1)解:设提示牌和公示栏的单价各是![]() 元,
元,![]() 元.
元.
由题得:![]()
解之得:![]()
答:提示牌和公示栏的单价各是30元,150元.
(2)设购买![]() 个公示栏,则购买提示牌(
个公示栏,则购买提示牌(![]() )个.
)个.
由题:![]()
不等式组解集为:![]()
∵![]() 是整数
是整数
∴![]() ,共有三种方案.
,共有三种方案.
方案1:购买12个公示栏,38个提示牌;
方案2:购买13个公示栏,37个提示牌;
方案3:购买14个公示栏,36个提示牌.
当购买12个公示栏,38个提示牌时,费用最少,最少费用为:![]() 元.
元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C、E是⊙O上的点, CD⊥AB,EF⊥AB,垂足分别为D、F,过点E作 EG⊥0C,垂足为G,延长EG交OA于H。
求证:
(1)HO·HF=HG·HE;
(2)FG=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
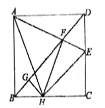
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .在以下四个结论中:①
.在以下四个结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长为12.其中正确的结论有__________(填序号)
的周长为12.其中正确的结论有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
对于任意一个三位数正整数n,如果n的各个数位上的数字互不相同,且都不为零,那么称这个数为“陌生数”,将一个“陌生数”的三个数位上的数字交换顺序,可以得到5个不同的新“陌生数”,把这6个陌生数的和与111的商记为M(n).例如n=123,可以得到132.213.231.312.321这5个新的“陌生数”,这6个“陌生数”的和为123+132+213+231+312+321=1332,因为![]() ,所以M(123)=12.
,所以M(123)=12.
(1)计算:M(125)和M(361)的值;
(2)设s和t都是“陌生数”,其中4和2分别是s的十位和个位上的数字,2和5分别是t的百位和个位上的数字,且t的十位上的数字比s的百位上的数字小2;规定:![]() .若
.若![]() ,则k的值是多少?
,则k的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,∠BAC=60,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD∶AB=AE∶AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45时,BE=![]() DE中,一定正确的有 .
DE中,一定正确的有 . 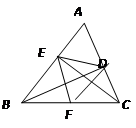
查看答案和解析>>
科目:初中数学 来源: 题型:
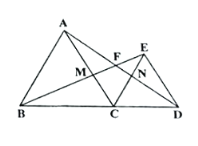
【题目】如图,己知点C是线段BD上一点,以BC、 DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD, BE相交于点F, AC和BE交于点M, AD, CE交于点N,(注:等边三角形的每一个内角都等于60° )
(1) 求证: AD=BE
(2) 线段CM与CN相等吗?请证明你的结论。
(3) 求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1= ![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论: ①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论: ①a= ![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com