
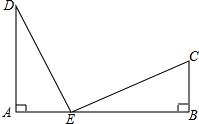
 如图,铁路上A、B两点相距17千米,C、D为两村庄,DA⊥AB于A,CB⊥AB于B.已知DA=12km,CB=5km,现要在铁路AB上建一个土产品收购站E,使得C.D两村到E站的距离相等,则E站应建在离A站多少km处?
如图,铁路上A、B两点相距17千米,C、D为两村庄,DA⊥AB于A,CB⊥AB于B.已知DA=12km,CB=5km,现要在铁路AB上建一个土产品收购站E,使得C.D两村到E站的距离相等,则E站应建在离A站多少km处?  云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
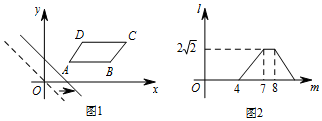
| A. | 5 | B. | 5$\sqrt{5}$ | C. | 8 | D. | 10$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
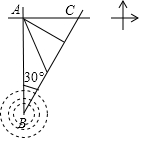 台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.
台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com