
【题目】有一边长为![]() 的等边
的等边![]() 游乐场,某人从边
游乐场,某人从边![]() 中点
中点![]() 出发,先由点
出发,先由点![]() 沿平行于
沿平行于![]() 的方向运动到
的方向运动到![]() 边上的点
边上的点![]() ,再由
,再由![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,又由点
,又由点![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,则此人至少要运动_______
,则此人至少要运动_______![]() ,才能回到点
,才能回到点![]() .如果此人从
.如果此人从![]() 边上意一点出发,按照上面的规律运动,则此人至少走______
边上意一点出发,按照上面的规律运动,则此人至少走______![]() ,就能回到起点.
,就能回到起点.
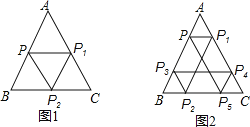
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
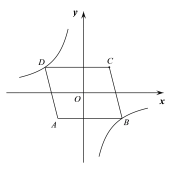
A.10B.18C.20D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.


(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E是以AB为直径的圆O上两点,且∠AED=45°,过点D作DC∥AB.
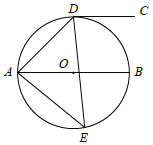
(1)请判断直线CD与圆O的位置关系,并说明理由;
(2)若圆O的半径为![]() ,
,![]() ,求AE的长;
,求AE的长;
(3)过点D作![]() ,垂足为F,直接写出线段AE、BE、DF之间的数量关系 .
,垂足为F,直接写出线段AE、BE、DF之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC于点M,且∠ADE=∠CDF.
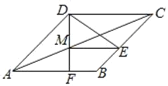
(1)求证:CE=AF;
(2)连接ME,若![]() =
=![]() ,AF=2,求
,AF=2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
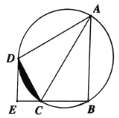
(1)用尺规作图作出圆心O;(保留作图痕迹,不写作法);
(2)求证:DE⊥BC;
(3)若OC=2CE=4,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.

(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD- DC- CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com