
【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.
![]()
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】小明家(记为A)、他上学的学校(记为B)、书店(记为C)依次坐落在一条东西走向的大街上,小明家位于学校西边250米处,书店位于学校东边100米处,小明中午放学后,到书店买本辅导书,然后回家吃中午饭,下午直接去学校上课.
(1)试用数轴表示出小明家(A)、学校(B)、书店(C)的位置;
(2)计算出小明家与书店的距离;
(3)小明从中午放学离校到下午上学到校一共走了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站相距240千米,从甲站开出一列慢车,速度为每小时80千米,从乙站开出一列快车,速度为每小时120千米.
(1)若两车同时开出,背向而行,则经过多长时间两车相距540千米?
(2)若两车同时开出,同向而行(快车在后),则经过多长时间快车可追上慢车?
(3)若两车同时开出,同向而行(慢车在后),则经过多长时间两车相距300千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,随机抽取3张,用抽到的三个数字作为边长,恰能构成三角形的概率是( )
A.![]() ?
?
B.![]() ?
?
C.![]() ?
?
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
【答案】(1)-195(2)2xy-2
【解析】试题分析:(1)利用平方差公式,完全平方公式简便计算.
(2)提取公因式,化简.
试题解析:
(1)原式=(100-1)2-(100+2)×(100-2)
=(1002-200+1)-(1002-4)=-200+5=-195.
(2)原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y=2(xy-1)=2xy-2.
【题型】解答题
【结束】
21
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(﹣1,4).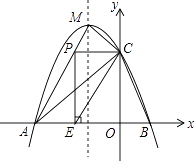
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD与△ACB面积相等时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将△PCE沿直线CE翻折,使点P的对应点P′与P、E、C处在同一平面内,请求出点P′坐标,并判断点P′是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:
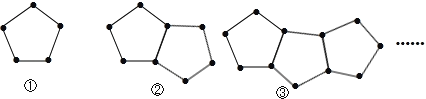
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com