
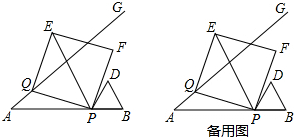
分析 (1)如图1,设PE交AG于点M,过点Q作QN⊥AP于N,在RT△ANQ中,tan∠GAB=$\frac{3}{4}$,设QN=3k,AN=4k,则AQ=5k,列出方程即可角问题.
(2)如图2中,过点Q作QH⊥AP于H,分三种情形①当AQ=AP时,②当AP=PQ时,③当AQ=PQ时,列出方程即可.
(3))①如图3中,当点F在直线PD上时,作QH⊥AB于H,②如图4中,当点F在直线PB上时,③如图5中,当点F在BD边上时,作QH⊥AB于H,FM⊥AB于M.
分别列出方程即可解决问题.
解答 解:(1)如图1,设PE交AG于点M.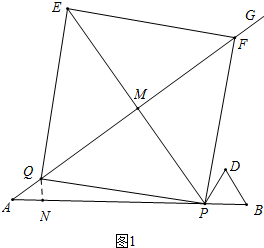
∵四边形PQEF是正方形,
∴PE⊥FQ,
∴当PE⊥AG时,点F在AG上,
∴PM=MQ,
过点Q作QN⊥AP于N,在RT△ANQ中,tan∠GAB=$\frac{3}{4}$,设QN=3k,AN=4k,则AQ=5k,
∴sin∠MAP=$\frac{3}{5}$,cos∠MAP=$\frac{4}{5}$,
∵AP=10-5t,
∴MQ═PM=AP•sin∠MAP=6-3t,AM=AP•cos∠MAP=8-4t,
∵AQ=5t,
∴5t+(6-3t)=8-4t,
∴t=$\frac{1}{3}$.
(2)如图2中,过点Q作QH⊥AP于H,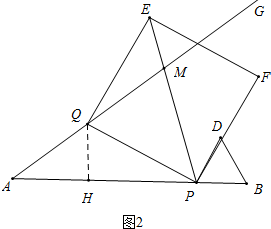
在RT△AQH中,AQ=5t,
∴AH=AQ•sin∠MAP=5t$•\frac{4}{5}$=4t,QH=AQ•sin∠MAP=3t,
∵AP=10-5t,
∴HP=10-9t,
在RT△PQH中,∵∠PHQ=90°,
∴PQ2=HQ2+PH2=(10-9t)2+(3t)2=90t2-180t+100,
①当AQ=AP时,10-5t=5t,解得t=1,
②当AP=PQ时,(10-5t)2=90t2-180t+100,解得t=$\frac{16}{13}$(或0舍弃),
③当AQ=PQ时,10-5t=3t,解得t=$\frac{10}{13}$,
综上所述,当△APQ是等腰三角形时,t的值为1s,$\frac{16}{13}$s,$\frac{10}{13}$s.
(3)①如图3中,当点F在直线PD上时,作QH⊥AB于H,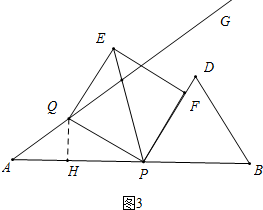
∵∠QOH+∠DPB=90°,∠DPB=60°,
∴∠QPH=30°,
∴PF=PQ=2QH=6t>5t,
∴PF>PD,
这种情形不符合题意.
②如图4中,当点F在直线PB上时,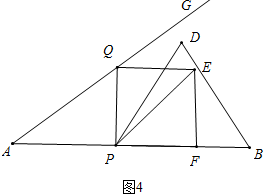
在RT△AQP中,∵AQ=5t.AP=4t,
又∵AP=10-5t,
∴4t=10-5t,
∴t=$\frac{10}{9}$,此时PQ=4t<5t,符合题意.
③如图5中,当点F在BD边上时,作QH⊥AB于H,FM⊥AB于M.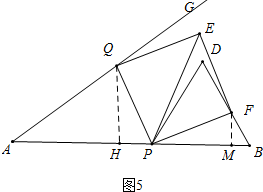
由△QPH≌△PFM,得到QH=PM=3t,HP=FN=10-5t-4t=10-9t,
在RT△FNB中,∵∠B=60°,
∴BM=$\frac{\sqrt{3}}{3}$FM=$\frac{\sqrt{3}}{3}$(10-9t),
∵PM+BM=PB,
∴3t+$\frac{\sqrt{3}}{3}$(10-9t)=5t,
∴t=$\frac{10}{9+2\sqrt{3}}$.
综上所述t=$\frac{10}{9}$s或$\frac{10}{9+2\sqrt{3}}$s时,点F落在△BPD的边上.
点评 本题考查四边形综合题、正方形的性质、等边三角形的性质、锐角三角函数、勾股定理.相似三角形的判定和性质等知识,解题的关键是学会分类讨论,学会利用图象解决问题,把问题转化为方程是思考,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
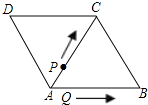 如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒
如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
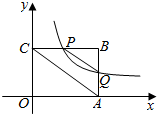 如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线y=$\frac{k}{x}$(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线y=$\frac{k}{x}$(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=0.05x | B. | y=3x | C. | y=60x | D. | y=0.05x+60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 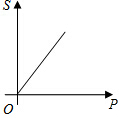 | B. | 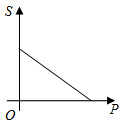 | C. | 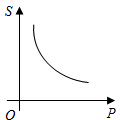 | D. | 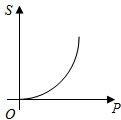 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
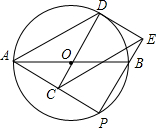 如图,AB是⊙O直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE.
如图,AB是⊙O直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com