
分析 首先提出问题,例如,求甲、乙两公司的人数分别是多少?则本题的等量关系是:乙公司的人均捐款-甲公司的人均捐款=40,根据这个等量关系可得出方程求解.
解答 问题:求甲、乙两公司的人数分别是多少?
解:设乙公司人数为x,则甲公司的人数为(1+20%)x,
根据题意得:$\frac{60000}{x}$-$\frac{60000}{(1+20%)x}$=40
解得:x=250
经检验x=250是原方程的根,
故(1+20%)×250=300(人),
答:甲公司为300人,乙公司250人.
点评 本题考查了分式方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}}{{b}^{2}}$ | B. | $\frac{a}{b}$ | C. | $\frac{a(a+b)}{b(a+b)}$ | D. | $\frac{{a}^{2}+1}{{b}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
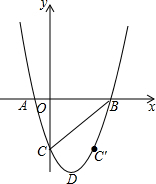 已知:抛物线y=x2-4x-m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.
已知:抛物线y=x2-4x-m(m>0)与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,C点关于抛物线对称轴的对称点为C′点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com