
 如图,已知反比例函数y=$\frac{k}{x}$在第一象限的图象过点A(1,3)和点C,点C与点A不重合,连结OA、OC,以OA、OC为边作?ABCO.
如图,已知反比例函数y=$\frac{k}{x}$在第一象限的图象过点A(1,3)和点C,点C与点A不重合,连结OA、OC,以OA、OC为边作?ABCO.分析 (1)由反比例函数y=$\frac{k}{x}$在第一象限的图象过点A(1,3),直接利用待定系数法求解即可求得答案;
(2)首先设点C的坐标为(x,y),然后由?ABCO为菱形,点C在反比例函数y=$\frac{3}{x}$上,可得x2+y2=12+32=10①,xy=3②,继而求得答案;
(3)首先连接AC,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,由S△AOC=S梯形ADEC+S△AOD-S△OCE,即可求得答案.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$在第一象限的图象过点A(1,3),
∴3=$\frac{k}{1}$,
解得:k=3;
(2)设点C的坐标为(x,y),
∵?ABCO是菱形,
∴OA=OC,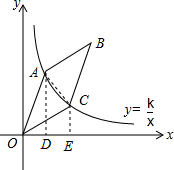 ∴x2+y2=12+32=10①,
∴x2+y2=12+32=10①,
∵点C在反比例函数y=$\frac{3}{x}$上,
∴xy=3②,
联立①②得:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴点C的坐标为(3,1);
(3)连接AC,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,
则AD=3,OD=1,OE=a,CE=$\frac{3}{a}$,S△AOD=S△OCE,
∴DE=OE-OD=a-1=2,
∴S△AOC=S梯形ADEC+S△AOD-S△OCE=S梯形ADEC=$\frac{1}{2}$(CE+AD)•DE=$\frac{1}{2}$×($\frac{3}{a}$+3)×(a-1)=$\frac{3{a}^{2}-3}{2a}$,
∵四边形ABCO是平行四边形,
∴S=2S△AOC=$\frac{3{a}^{2}-3}{a}$.
点评 此题属于反比例函数综合题.考查了待定系数求函数解析式、平行四边形的性质以及菱形的性质.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①或② | B. | ②或③ | C. | ③或④ | D. | ①或④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,双曲线$y=\frac{k}{x}(x>0)$与矩形AOBC的两边交于M(4,2)、N两点,且四边形MONC的面积是8.
如图,在直角坐标系中,双曲线$y=\frac{k}{x}(x>0)$与矩形AOBC的两边交于M(4,2)、N两点,且四边形MONC的面积是8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}\sqrt{10}$ | B. | 25$\sqrt{10}$ | C. | $\sqrt{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com