Question

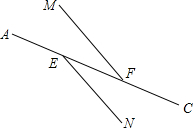
17．如图，线段AC上有两点E、F，已知AE=CF，FM∥EN，点D在FM上，连接AD构成△AFD，点B在EN上，连接CB构成△CEB，那么添加下列一个条件后，无法判定△ADF≌△CBE的是（　　）

• A． ∠FAD=∠ECB
• B． AD=CB
• C． BE=DF
• D． AD∥BC

Answer 1

分析 首先根据平行线的性质可得∠MFA=∠BEC，由等式的性质可得AF=EC，再分别添加四个选项中的条件，利用全等三角形的判定定理分别进行分析即可．

解答 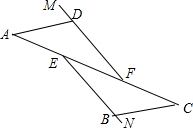解：∵FM∥EN，
∴∠MFA=∠BEC，
∵AE=CF，
∴AF=EC，
A、添加∠FAD=∠ECB可利用ASA判定△ADF≌△CBE；
B、添加AD=CB不能判定△ADF≌△CBE；
C、添加BE=DF可利用SAS判定△ADF≌△CBE；
D、添加AD∥BC可得∠A=∠C，可利用ASA判定△ADF≌△CBE；
故选：B．

点评 本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．