
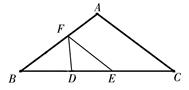
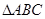 中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).
中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).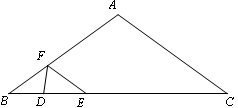
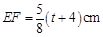 ;(2)
;(2)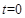 、
、 或
或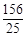 秒;(3)
秒;(3) cm2
cm2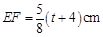 .
. 时,有
时,有

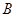 与点
与点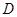 重合,∴
重合,∴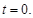 …
…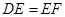 时
时
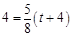 ,解得:
,解得:
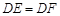 时,有
时,有
 ,即
,即 ,解得:
,解得: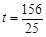 .
. 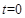 、
、 或
或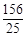 秒时,△
秒时,△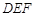 为等腰三角形;
为等腰三角形; cm2
cm2  ∥
∥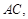 ∴△
∴△ ∽△
∽△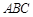 .
.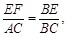 ∴
∴
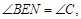 ∴△
∴△ ∽△
∽△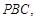 ∴
∴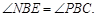
 沿直线BP运动,MN也随之平移.
沿直线BP运动,MN也随之平移. 、
、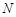 分别是
分别是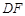 、
、 的中点,∴
的中点,∴ ∥DE,且ST=MN=
∥DE,且ST=MN=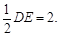
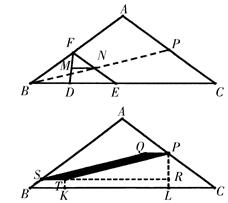
 (0+4)=
(0+4)=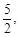 TK=
TK=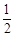 EF·
EF·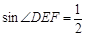 ·
·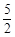 ·
·
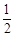 AC·
AC·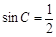 ·10·
·10·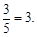
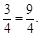
 即整个运动过程中,MN所扫过的图形的面积为
即整个运动过程中,MN所扫过的图形的面积为 cm2.
cm2.

 习题精选系列答案
习题精选系列答案科目:初中数学 来源:不详 题型:解答题
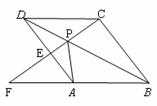
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.55 . | B.100. | C.25. | D.30. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
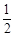 . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
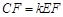 ,则k = ;
,则k = ;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
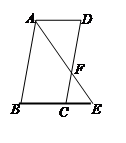
| A.1对; | B.2对; | C.3对; | D.4对. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com