练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．下列由2和3组成的四个算式中，值最小的是（　　）
    A．2-3B．2÷3C．23D．2-3

    分析 各项计算得到结果，即可做出比较．

    解答 解：A、原式=-1；
    B、原式=$\frac{2}{3}$；
    C、原式=8；
    D、原式=$\frac{1}{8}$，
    ∴-1＜$\frac{1}{8}$＜$\frac{2}{3}$＜8，
    则值最小的为2-3，
    故选A

    点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．若y=（x+2b）2-4b2+a2+3b和y=2（x-4）2-2b-1有相同的顶点，则a=5或-5，b=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．汽车油箱中的余油量Q（升）与它行驶的时间t（小时）之间的关系如下表：
    余油量Q/L6050403020…
    行驶时间t/h02468…
    （1）求油箱中的余油量Q与行驶时间t的函数关系式；
    （2）从开始算起，如果汽车每小时行驶40千米，当油箱中的油耗尽时，该汽车行驶了多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=6，BC=8，AB=3$\sqrt{3}$，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒（t＞0）．
    （1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．
    （2）当BP=1时，求△EPQ与梯形ABCD重叠部分的面积．
    （3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

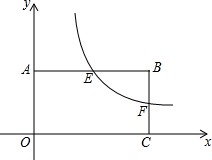    18．如图，反比例函数$y=\frac{k}{x}（k＞0）$的图象与矩形ABCO的两边相交于E，F两点，若E是AB的中点，S△BEF=3，则k的值为12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．已知三角形的两边长分别为3和5，则此三角形的周长不可能是（　　）
    A．11B．13C．15D．17

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x-y=2}\\{ax+y=3a-1}\end{array}\right.$的解满足x+y=1，则a的值为$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算
    （1）$（3\sqrt{48}-2\sqrt{27}）÷\sqrt{3}$；
    （2）$（\sqrt{3}+1）（\sqrt{3}-1）-\sqrt{{{（-3）}^2}}+\frac{1}{{2-\sqrt{5}}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．河的一旁有两个村子A、B，要在河边建一水泵站引水到村里．一村民画了一张图，以直线l表示一条河，求作一点P，使P到A、B的距离和最短，作出P点，并用几何语言叙述你的理由．

    查看答案和解析>>

    同步练习册答案