
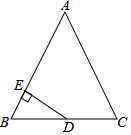
 如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )| A. | $\frac{10}{13}$ | B. | $\frac{15}{13}$ | C. | $\frac{45}{13}$ | D. | $\frac{60}{13}$ |
分析 首先连接AD,由△ABC中,AB=AC=13,BC=10,D为BC中点,利用等腰三角形的三线合一的性质,即可证得:AD⊥BC,然后利用勾股定理,即可求得AD的长,然后利用面积法来求DE的长.
解答 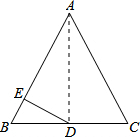 解:连接AD,
解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=$\frac{1}{2}$BC=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=12,
又∵DE⊥AB,
∴$\frac{1}{2}$BD•AD=$\frac{1}{2}$AB•ED,
∴ED=$\frac{BD•AD}{AB}$=$\frac{5×12}{13}$=$\frac{60}{13}$,
故选D.
点评 此题考查了等腰三角形的性质以及勾股定理.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-10% | B. | a•10% | C. | (1-10%)a | D. | (1+10%)a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=6,c=2,d=4 | B. | a=1,b=$\sqrt{2}$,c=2$\sqrt{2}$,d=4 | ||
| C. | a=4,b=5,c=8,d=10 | D. | a=2,b=3,c=4,d=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
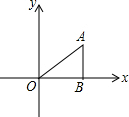 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )| A. | (-1,-$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$)或(-2,0) | C. | (-$\sqrt{3}$,1)或(0,-2) | D. | (-$\sqrt{3}$,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
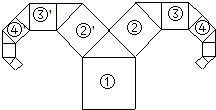 如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.
如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com