
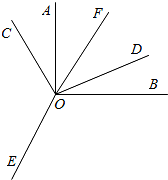
 如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:
如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ②③④ |
分析 由∠AOB=∠COD=90°根据同角的余角相等得到∠AOC=∠BOD,而∠COE=∠BOE,即可判断①正确;
由∠AOD+∠COB=∠AOD+∠AOC+90°,而∠AOD+∠AOC=90°,即可判断②正确;
由∠COB-∠DOE=∠AOC+90°-∠BOD-∠BOE=90°-∠BOE≠90°,即可判断③不正确;
由OF平分∠AOD得∠AOF=∠DOF,由①得∠AOE=∠DOE,根据周角的定义得到∠AOF+∠AOE=∠DOF+∠DOE=180°,即点F、O、E共线,又∠COE=∠BOE,即可判断④正确.
解答 解:∵∠AOB=∠COD=90°,即∠AOD+∠BOD=∠AOD+AOC=90°,
∴∠BOD=∠AOC,
又∵∠COE=∠BOE,
∴∠AOC+∠COE=∠BOD+∠BOE,即∠AOE=∠DOE,故①正确;
∠AOD+∠COB=∠AOD+∠AOC+90°=90°+90°=180°,故②正确;
∠COB-∠DOE=∠AOC+90°-∠BOD-∠BOE=90°-∠BOE≠90°,故③错误;
∵OF平分∠AOD,
∴∠AOF=∠DOF,
而∠AOE=∠DOE,
∴∠AOF+∠AOE=∠DOF+∠DOE=180°,即点F、O、E共线,
∵∠COE=∠BOE,
∴∠COE+∠BOF=180°,故④正确;
故选:A.
点评 本题考查了角度的计算,同角(等角)的余角相等.也考查了角平分线的定义,熟练掌握补余角的性质和角平分线的定义是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
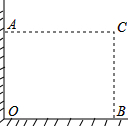 在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成底面为矩形的储仓,且底面矩形AOBC的面积为96m2
在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成底面为矩形的储仓,且底面矩形AOBC的面积为96m2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8000(1+x)2=7000 | B. | 8000(1-x)2=7000 | C. | 7000(1-x)2=8000 | D. | 7000(1+x)2=8000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.
如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这两个数的相反数的商等于它们商的相反数 | |
| B. | 这两个数的差的相反数等于它们相反数的差 | |
| C. | 这两个数的绝对值的积等于它们的积的绝对值 | |
| D. | 这两个数的商的绝对值等于它们绝对值的商 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数轴上的点只能表示整数 | |
| B. | 数轴上的点只能表示分数 | |
| C. | 数轴上的点只能表示有理数 | |
| D. | 所有有理数和无理数都可以用数轴上的点表示出来 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
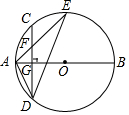 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com