
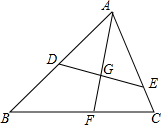
 如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.分析 (1)可得到三组三角形相似;
(2)先利用两组对应边的比相等且夹角对应相等的两个三角形相似证明△ADE∽△ACB,则∠ADG=∠C,再利用有两组角对应相等的两个三角形相似证明△ADG∽△ACF,然后利用相似比和比例的性质求$\frac{AG}{GF}$的值.
解答 解:(1)△ADG∽△ACF,△AGE∽△AFB,△ADE∽△ACB;
(2)∵$\frac{AE}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$,$\frac{AD}{AC}$=$\frac{2}{3}$,
∴$\frac{AE}{AB}$=$\frac{AD}{AC}$,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB,
∴∠ADG=∠C,
∵AF为角平分线,
∴∠DAG=∠FAE
∴△ADG∽△ACF,
∴$\frac{AG}{AF}$=$\frac{AD}{AC}$=$\frac{2}{3}$,
∴$\frac{AG}{GF}$=2.
点评 本题考查了相似三角形的判断:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
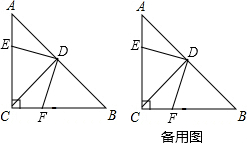 在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.
在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E是边AC上的一动点,点F是边BC上的一动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.
在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )| A. | 0.1 | B. | 0.17 | C. | 0.33 | D. | 0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com