
 (x>0)与矩形AOBC的两边交于M(4,2)、N两点.且四边形MONC的面积是8.
(x>0)与矩形AOBC的两边交于M(4,2)、N两点.且四边形MONC的面积是8. 的MN段(含端点)上移动时.△OFC随之变动.是否存在点P,使△OFG是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
的MN段(含端点)上移动时.△OFC随之变动.是否存在点P,使△OFG是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
 的图象上,
的图象上, ,
, |k|=4,
|k|=4,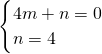 ,
,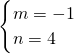 ,
, 的MN段(含端点)上的一动点,由点P向x轴、y轴作垂线PE、PD.垂足是E、D,与线段AB分别交于F、G,
的MN段(含端点)上的一动点,由点P向x轴、y轴作垂线PE、PD.垂足是E、D,与线段AB分别交于F、G,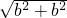 =
= b,BG=
b,BG= =
= a,
a, b•
b• a=2ab=2×8=16=OA•OB,
a=2ab=2×8=16=OA•OB,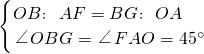
 •OB•BN=4,OB=4,
•OB•BN=4,OB=4, 的MN段(含端点)上移动,M(4,2),
的MN段(含端点)上移动,M(4,2),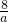 ,
,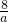 -4=0,a2-4a+8=0,△<0,无解;
-4=0,a2-4a+8=0,△<0,无解; ,P点坐标为(2
,P点坐标为(2 ,2
,2 );
);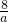 代入,整理得a3-8a2+24a-32=0,
代入,整理得a3-8a2+24a-32=0,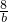 代入,整理得b3-8b2+24b-32=0,
代入,整理得b3-8b2+24b-32=0, ,2
,2 )或(4,2)或(2,4),能使△OFG是等腰三角形.
)或(4,2)或(2,4),能使△OFG是等腰三角形. ,运用待定系数法求出反比例函数的解析式,再根据反比例函数比例系数k的几何意义得出S△AOM=S△BON=
,运用待定系数法求出反比例函数的解析式,再根据反比例函数比例系数k的几何意义得出S△AOM=S△BON= |k|=4,则矩形AOBC的面积为16,又OA=4,根据面积公式得出OB=4,则矩形AOBC是正方形;
|k|=4,则矩形AOBC的面积为16,又OA=4,根据面积公式得出OB=4,则矩形AOBC是正方形;

科目:初中数学 来源: 题型:
 sin∠BOA=
sin∠BOA=| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| m | x |
 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在直角坐标平面内,点A的坐标为(3,0),第一象限内的点P在直线y=2x上,∠PAO=45度.
(1)求点P的坐标;
(2)如果二次函数的图像经过P、O、A三点,求这个二次函数的解析式,并写出它的图像的顶点坐标M;
(3)如果将第(2)小题中的二次函数的图像向上或向下平移,使它的顶点落在直线y=2x上的点Q处,求△APM与△APQ的面积之比.
 |
查看答案和解析>>
科目:初中数学 来源:2013年上海市中考数学模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com