
分析 (1)去括号,移项,合并同类项,系数化为1,即可求得不等式的解集;
(2)首先解每个不等式,然后确定两个不等式的解集的公共部分,即是不等式组的解集.
解答 解:(1)3(x+1)<4(x-2)-3
3x+3<4x-8-3
3x-4x<-8-3-3
-x<-14
x>14
在数轴上表示出来为:
(2)$\left\{\begin{array}{l}{2x-(x-2)>4}\\{\frac{1-2x}{3}≤x-1}\end{array}\right.$
解不等式①得x>2,
解不等式②得x≥$\frac{4}{5}$,
在数轴上表示为:
所以不等式组的解集为x>2.
点评 此题考查不等式与不等式组的解法,利用数轴直观表示解集是一种常用解决问题的方法.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=50}\\{10(x+y)=320}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=50}\\{6x+y=320}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=50}\\{6x+10y=320}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=50}\\{10x+6y=320}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数y=$\frac{k}{x}$的图象经过点E,G两点,则k的值为5.
如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数y=$\frac{k}{x}$的图象经过点E,G两点,则k的值为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
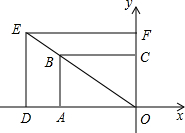 如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )| A. | (3.6,2.4) | B. | (-3,2.4) | C. | (-3.6,2) | D. | (-3.6,2.4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com