
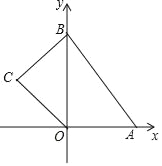
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(﹣2![]() ,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
(1)填空:AB的长是 ,BC的长是 ;
(2)当t=3时,求S的值;
(3)当3<t<6时,设点N的纵坐标为y,求y与t的函数关系式;
(4)若S=![]() ,请直接写出此时t的值.
,请直接写出此时t的值.
【答案】(1)10,6(2)6(3)y=![]() t(4)若S=
t(4)若S=![]() ,此时t的值8s或
,此时t的值8s或![]() s或
s或![]() s
s
【解析】
试题分析:(1)利用勾股定理即可解决问题;
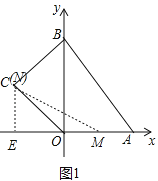
(2)如图1中,作CE⊥x轴于E.连接CM.当t=3时,点N与C重合,OM=3,易求△OMN的面积;
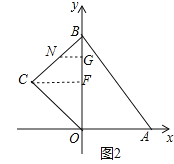
(3)如图2中,当3<t<6时,点N在线段BC上,BN=12﹣2t,作NG⊥OB于G,CF⊥OB于F.则F(0,4).由GN∥CF,推出![]() ,即
,即![]() ,可得BG=8﹣
,可得BG=8﹣![]() t,由此即可解决问题;
t,由此即可解决问题;
(4)分三种情形①当点N在边长上,点M在OA上时.②如图3中,当M、N在线段AB上,相遇之前.作OE⊥AB于E,则OE=![]() =
=![]() ,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;
,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;
试题解析:(1)在Rt△AOB中,∵∠AOB=90°,OA=6,OB=8,∴AB=![]() =
=![]() =10.
=10.
BC=![]() =6.
=6.
(2)如图1中,作CE⊥x轴于E.连接CM.
∵C(﹣![]() ,4),∴CE=4OE=
,4),∴CE=4OE=![]() ,在Rt△COE中,OC=
,在Rt△COE中,OC=![]() =
=![]() =6,当t=3时,点N与C重合,OM=3,∴S△ONM=
=6,当t=3时,点N与C重合,OM=3,∴S△ONM=![]() OMCE=
OMCE=![]() ×3×4=6,即S=6.
×3×4=6,即S=6.
(3)如图2中,当3<t<6时,点N在线段BC上,BN=12﹣2t,作NG⊥OB于G,CF⊥OB于F.则F(0,4).∵OF=4,OB=8,∴BF=8﹣4=4,∵GN∥CF,∴![]() ,即
,即![]() ,∴BG=8﹣
,∴BG=8﹣![]() t,∴y=OB﹣BG=8﹣(8﹣
t,∴y=OB﹣BG=8﹣(8﹣![]() t)=
t)=![]() t.
t.
(4)①当点N在边长上,点M在OA上时,![]()
![]() tt=
tt=![]() ,解得t=
,解得t=![]() (负根已经舍弃).
(负根已经舍弃).
②如图3中,当M、N在线段AB上,相遇之前.
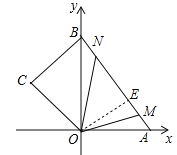
作OE⊥AB于E,则OE=![]() =
=![]() ,由题意
,由题意![]() [10﹣(2t﹣12)﹣(t﹣6)]
[10﹣(2t﹣12)﹣(t﹣6)] ![]() =
= ![]() ,解得t=8,同法当M、N在线段AB上,相遇之后.
,解得t=8,同法当M、N在线段AB上,相遇之后.
由题意![]() [(2t﹣12)+(t﹣6)﹣10]
[(2t﹣12)+(t﹣6)﹣10] ![]() =
= ![]() ,解得t=
,解得t=![]() .
.
综上所述,若S=![]() ,此时t的值8s或
,此时t的值8s或![]() s或
s或![]() s.
s.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
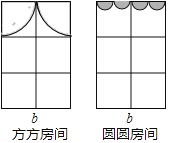
【题目】方方和圆圆房间的窗户的装饰物如图中的阴影部分,它们分别由两个四分之一圆和四个半圆组成(半径部分分别相同).求:
(1)方方房间窗户饰物的面积是 ,圆圆房间窗户饰物的面积是 .
(2)若长方形窗户的长为a,宽为b,请分别说明他们的窗户能射进阳光的面积是多少(窗框面积不计)?并说明谁的窗户射进阳光面积较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
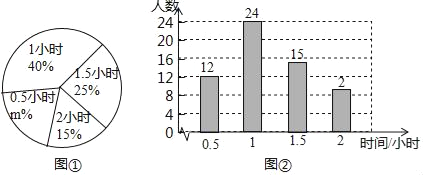
【题目】某校为了解学生每天参加户外活动的情况,随机抽查了一部分学生每天参加户外活动的时间情况,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题;
(Ⅰ)在图①中,m的值为 ,表示“2小时”的扇形的圆心角为 度;
(Ⅱ)求统计的这组学生户外运动时间的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直接开平方法解下列方程:
(1)(x﹣2)2=3;
(2)2(x﹣3)2=72;
(3)9(y+4)2﹣49=0;
(4)4(2y﹣5)2=9(3y﹣1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(1-2m)x+m+1(m≠![]() ),函数值y随自变量x值的增大而减小.
),函数值y随自变量x值的增大而减小.
(1)求m的取值范围;
(2)在平面直角坐标系xOy中,这个函数的图象与x轴的交点M位于x轴的正半轴还是负半轴?请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com