
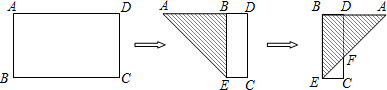
如图,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(但不与顶点重合),若EF将矩形ABCD分成面积相等的两部分,设AB=a,AD=b,BE=x.(1)求证:AF=EC;(2)用剪刀将该纸片沿直线EF剪开后,再将梯形纸片ABEF沿AB对称翻折,平移拼接在梯形ECDF的下方,使一底边重合,一腰落在DC的延长线上,拼接后,下方梯形记作![]() .①当x∶b为何值时,直线
.①当x∶b为何值时,直线![]() 经过原矩形的一个顶点.②在直线
经过原矩形的一个顶点.②在直线![]() 经过原矩形的一个顶点的情况下,连接
经过原矩形的一个顶点的情况下,连接![]() ,直线
,直线![]() 与EF是否平行?你若认为平行,请给予证明;你若认为不平行,试探究当a与b有何种数量关系时,它们就垂直.
与EF是否平行?你若认为平行,请给予证明;你若认为不平行,试探究当a与b有何种数量关系时,它们就垂直.

|
解答 (1)∵EF将矩形ABCD分成面积相等的两部分,则有
x+AF=b-x+b-AF,AF=b-x. 又 EC=b-x,∴AF=EC.(2)①当直线
∵ DC=当直线
∵ DC=∴ 2EC=即 2(b-x)=x+b,解得x∶b=1∶3.∴当 x∶b的值为②当直线
证明如下:连结 BF.∵FD∥BE,FD=BE,∴四边形BFDE是平行四边形,∴ BF∥DE,BF=DE.又 DC=又 BF∥当直线
∵∠ FEM=∠EFA=若∠ BEG=当∠ BEG=∴ ∵ a>0,b>0,∴ |
|
注意:本题难度较大,解本题的关键是看懂题意,如“将梯形 ABEF沿AB对称翻折”,“平移拼接在梯形ECDF的下方”的意义,并画出正确的图形. |


科目:初中数学 来源: 题型:
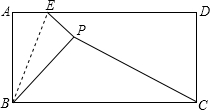 (2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.
(2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
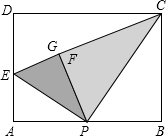 如图,有一张矩形纸片ABCD,AB=4,AD=3,P为AB中点,点E在AD上,将△PBC,△PAE翻折分别得到△PCF和△PEG,折痕分别为PC、PE,且点F在PG上,则AE长为
如图,有一张矩形纸片ABCD,AB=4,AD=3,P为AB中点,点E在AD上,将△PBC,△PAE翻折分别得到△PCF和△PEG,折痕分别为PC、PE,且点F在PG上,则AE长为| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com