
有下列4个命题:
①方程 的根是
的根是 和
和 .
.
②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD= ,则CD=3.
,则CD=3.
③点P(x,y)的坐标x,y满足x2+y2+2x﹣2y+2=0,若点P也在 的图象上,则k=﹣1.
的图象上,则k=﹣1.
④若实数b、c满足1+b+c>0,1﹣b+c<0,则关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x0满足﹣1<x0<1.
上述4个命题中,真命题的序号是 .
①②③④
解析试题分析:①解方程可知,方程 的根是
的根是 和
和 。此命题正确。
。此命题正确。
②∵在△ABC中,∠ACB=90°,CD⊥AB于D, AD=4,BD= ,
,
∴根据射影定理CD 2=AD×BD,解得CD=3。故此命题正确。
③∵点P(x,y)的坐标x,y满足x2+y2+2x﹣2y+2=0,
∴(x+1)2+(y﹣1)2=0,解得:x=﹣1,y=1。∴xy=﹣1。
∵点P也在 的图象上,∴k=﹣1。故此命题正确。
的图象上,∴k=﹣1。故此命题正确。
④∵实数b、c满足1+b+c>0,1﹣b+c<0,
∴y=x2+bx+c的图象如图所示,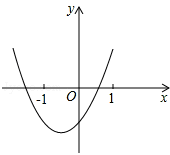
∴关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x0满足﹣1<x0<1。故此选项正确。
综上所述,真命题的序号是①②③④。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,
给出下列命题:
①abc<0;②b>2a;③a+b+c=0
④ax2+bx+c=0的两根分别为﹣3和1;
⑤8a+c>0.其中正确的命题是 .
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量 箱与销售价
箱与销售价 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价 (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
我市高新技术开发区的某公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-投资成本)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该公司希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利不低于1842元,请你确定此时销售单价的范围.在此情况下,要使产品销售量最大,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.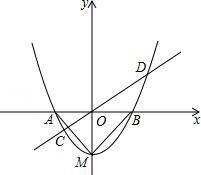
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com