
 如图,在△ABC中,∠ACB=90°,AC=8,CB=6,点D在线段CB的延长线上,且BD=2,点P从点D出发沿着DC向终点C以每秒1个单位的速度运动,同时点Q从点C出发沿着折线C-B-A往终点A以每秒2个单位的速度运动.以PQ为直径构造⊙O,设运动的时间为t(t≥0)秒.
如图,在△ABC中,∠ACB=90°,AC=8,CB=6,点D在线段CB的延长线上,且BD=2,点P从点D出发沿着DC向终点C以每秒1个单位的速度运动,同时点Q从点C出发沿着折线C-B-A往终点A以每秒2个单位的速度运动.以PQ为直径构造⊙O,设运动的时间为t(t≥0)秒.分析 (1)由题意BQ=BC-CQ=6-2t;
(2)分两种情况讨论:①当P,Q还未相遇时,如图1,②当P,Q相遇后,如图2,分别构建方程即可;
(3)①分三种情形讨论i)当点O在∠B的角平分线上时,如图3.ii)当点O在∠C的角平分线上时,如图4,作QG⊥AC于G,OF⊥AC于F,QH⊥BC于H.iii)当点O在∠A的角平分线上时,如图5,作∠A的角平分线交BC于点H,过点H做HI⊥AB于I.分别构建方程即可.
②由题意点O的运动路径为(6-4-$\frac{1}{2}$)+$\sqrt{(\frac{11}{2})^{2}+{4}^{2}}$=$\frac{3+\sqrt{185}}{2}$.
解答 解:(1)由题意BQ=BC-CQ=6-2t,
故答案为6-2t.
(2)分两种情况讨论:
①当P,Q还未相遇时,如图1,
CQ=2t,DP=t,QP=8-3t,OE=$\frac{1}{2}$QP=$\frac{8-3t}{2}$,
OB=BP+OP=$\frac{8-3t}{2}$+$\frac{2(t-2)}{2}$=$\frac{4-t}{2}$,
∵⊙O与AB相切,
∴OE⊥AB,
∵sin∠ABC=$\frac{OE}{OB}$=$\frac{AC}{AB}$,
∴$\frac{\frac{8-3t}{2}}{\frac{4-t}{2}}$=$\frac{4}{5}$,解得t=$\frac{24}{11}$.
②当P,Q相遇后,如图2,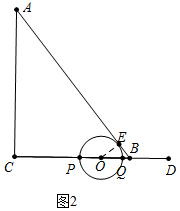
BQ=6-2t,PQ=BP-BQ=(t-2)-(6-2t)=3t-8,
OE=$\frac{1}{2}$QP=$\frac{3t-8}{2}$,OB=OQ+BQ=$\frac{4-t}{2}$,
∵⊙O与AB相切,∴OE⊥AB,
∵sin∠ABC=$\frac{OE}{OB}$=$\frac{AC}{AB}$,
∴$\frac{\frac{3t-8}{2}}{\frac{4-t}{2}}$=$\frac{4}{5}$,解得t=$\frac{56}{19}$.
综上所述,满足条件的t的值有t=$\frac{24}{11}$s或$\frac{56}{19}$s.
(3)①i)当点O在∠B的角平分线上时,如图3,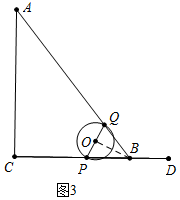
可得BQ=BP,即2t-6=t-2,解得t=4.
ii)当点O在∠C的角平分线上时,如图4,作QG⊥AC于G,OF⊥AC于F,QH⊥BC于H.
则GQ=AQ•sin∠BAC=$\frac{3}{5}$AQ=$\frac{3(16-2t)}{5}$,
同理可得GC=QH=$\frac{4}{5}$BQ=$\frac{4(2t-6)}{5}$,
在梯形CPQG中,OF是中位线,则OF=$\frac{1}{2}$(GQ+CP)
=$\frac{1}{2}$[$\frac{3(16-2t)}{5}$+(8-t)]=$\frac{88-11t}{10}$,
∵点O在∠C的角平分线上,∴CF=OF.
$\frac{88-11t}{10}$=$\frac{2(2t-6)}{5}$,解得t=$\frac{112}{19}$.
iii)当点O在∠A的角平分线上时,如图5,作∠A的角平分线交BC于点H,过点H做HI⊥AB于I,
则HI=CH.
∵sin∠ABC=$\frac{HI}{HB}=\frac{AC}{AB}$,则$\frac{HI}{HB}$=$\frac{4}{5}$,
∴CH=HI=$\frac{8}{3}$,∴tan∠CAH=$\frac{1}{3}$,
由ii)中得OF=(GQ+CP)=$\frac{88-11t}{10}$,
CF=$\frac{2(2t-6)}{5}$,AF=AC-CF=$\frac{52-4t}{5}$,
∴tan∠CAH=$\frac{OF}{AF}=\frac{{\frac{88-11t}{10}}}{{\frac{52-4t}{5}}}=\frac{1}{3}$,解得t=$\frac{32}{5}$.
综上所述,当t=4s或$\frac{112}{19}$s或$\frac{32}{5}$s时,点O会出现在△ABC的内角平分线上.
②由题意点O的运动路径为(6-4-$\frac{1}{2}$)+$\sqrt{(\frac{11}{2})^{2}+{4}^{2}}$=$\frac{3+\sqrt{185}}{2}$.
点评 本题考查圆综合题、解直角三角形、锐角三角函数、角平分线的性质、切线的判定和性质等知识,解题的关键是学会添加常用辅助线,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a-b+c<0;③2a+b-c<0;④4a+2b+c>0,⑤若点(-$\frac{2}{3}$,y1)和($\frac{7}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②③④(填入正确结论的序号)
已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a-b+c<0;③2a+b-c<0;④4a+2b+c>0,⑤若点(-$\frac{2}{3}$,y1)和($\frac{7}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②③④(填入正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
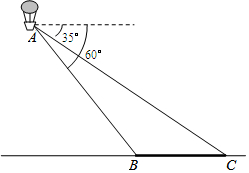 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.
如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A($\sqrt{3}$,0),点B(0,3),点O(0,0)
将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A($\sqrt{3}$,0),点B(0,3),点O(0,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com