
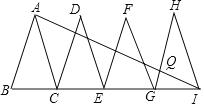
【题目】如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交GH于点Q.
(1)求证:△IAB∽△ACB;
(2)求HQ:QG的值.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
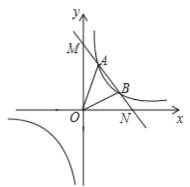
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点A(
的图象交于点A(![]() )、
)、![]() 两点,与坐标轴分别交于M、N两点.
两点,与坐标轴分别交于M、N两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 中
中![]() 的取值范围是____________;
的取值范围是____________;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据![]() )( )
)( )
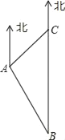
A. 7.3海里B. 10.3海里C. 17.3海里D. 27.3海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.

(1)小华的问题解答: ;
(2)小明的问题解答: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2+
x2+![]() x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<
x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<![]() )上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
(1)点A,B,D的坐标分别为 , , ;
(2)如图①,抛物线翻折后,点D落在点E处.当点E在△ABC内(含边界)时,求t的取值范围;
(3)如图②,当t=0时,若Q是“M”形新图象上一动点,是否存在以CQ为直径的圆与x轴相切于点P?若存在,求出点P的坐标;若不存在,请说明理由.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/28/2213337932849152/2214008649842688/STEM/890e59b444e5404588b8511540e03e41.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=12cm,BC=16cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为2cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为4cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
如图1,在等边△ABC中,AB=9,⊙C半径为3,P为圆上一动点,连结AP,BP,求AP+![]() BP的最小值
BP的最小值
(1)尝试解决:
为了解决这个问题,下面给出一种解题思路,通过构造一对相似三角形,将![]() BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
如图2,连结CP,在CB上取点D,使CD=1,则有![]()
又∵∠PCD=∠
△ ∽△
∴![]()
∴PD=![]() BP
BP
∴AP+![]() BP=AP+PD
BP=AP+PD
∴当A,P,D三点共线时,AP+PD取到最小值
请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为 .
BP的最小值为 .
(2)自主探索:
如图3,矩形ABCD中,BC=6,AB=8,P为矩形内部一点,且PB=4,则![]() AP+PC的最小值为 .(请在图3中添加相应的辅助线)
AP+PC的最小值为 .(请在图3中添加相应的辅助线)
(3)拓展延伸:
如图4,在扇形COD中,O为圆心,∠COD=120°,OC=4.OA=2,OB=3,点P是![]() 上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
上一点,求2PA+PB的最小值,画出示意图并写出求解过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
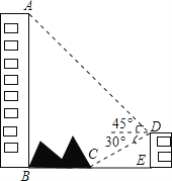
【题目】 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解决农民工子女就近入学问题,我市第一小学计划2012年秋季学期扩大办学规模.学校决定开支八万元全部用于购买课桌凳、办公桌椅和电脑,要求购买的课桌凳与办公桌椅的数量比为20:1,购买电脑的资金不低于16000元,但不超过24000元.已知一套办公桌椅比一套课桌凳贵80元,用2000元恰好可以买到10套课桌凳和4套办公桌椅.(课桌凳和办公桌椅均成套购进)
(1)一套课桌凳和一套办公桌椅的价格分别为多少元?
(2)求出课桌凳和办公桌椅的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com