
分析 根据连续偶数相差是2,设中间的偶数是x,则另外两个是x-2,x+2根据勾股定理即可求得直角三角形的三边长,再根据三角形周长和面积公式求解即可.
解答 解:设中间的偶数是x,则另外两个是x-2,x+2,根据勾股定理,得
(x-2)2+x2=(x+2)2,
x2-4x+4+x2=x2+4x+4,
x2-8x=0,
x(x-8)=0,
解得x=8或0(0不符合题意,应舍去),
所以它的三边是6,8,10.
6+8+10=24,
6×8÷2=24.
答:它的三边之和为24,面积为24.
故答案为:24,24.
点评 此题主要考查了勾股定理,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.


科目:初中数学 来源: 题型:解答题
| 原质量 | 27 | 24 | 23 | 28 | 21 | 26 | 22 | 27 |
| 与基准数的差距 | 1 | -2 | -3 | 2 | -5 | 0 | -4 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
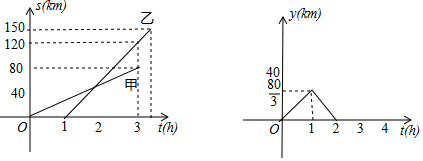
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
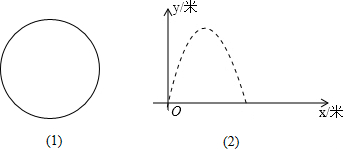
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com