练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知在△ABC中，∠A＝60°，∠C＝90°，将△ABC绕点B顺时针旋转150°，得到△DBE．请仅用无刻度的直尺，按要求画图（保留画图痕迹，在图中标出字母，并在图下方表示出所画图形）．

    （1）在图①中，画一个等边三角形；

    （2）在图②中，画一个等腰直角三角形．

    【答案】（1）见解析；（2）见解析．

    【解析】

    （1）如图①中，延长EB交AC的延长线于F，可得∠A=∠ABF=60°，故△ABF为等边三角形．
    （2）如图②中，连接AD交EB于H，由题意可知AB=BD，∠ABC=30°，故∠ADB=∠BAD=15°，可求得∠EDH=45°，即可得△EDH为等腰直角三角形．

    （1）如图①中，延长EB交AC的延长线于F．△ABF即为所求．

    （2）如图②中，连接AD交EB于H，△EDH即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个盒子里有3个相同的小球，将3个小球分别标示号码1、2、3，每次从盒子里随机取出1个小球且取后放回，预计取球10次．若规定每次取球时，取出的号码即为得分，则前八次的取球得分情况如下表所示

    次数

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    得分

    2

    1

    1

    2

    2

    3

    2

    3

    （1）设第1次至第8次取球得分的平均数为，求的值：

    （2）求事件“第9次和第10次取球得分的平均数等于”发生的概率；（列表法或树状图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若整数a使关于x的分式方程的解为整数，且使关于y的不等式组有解，且最多有4个整数解，则符合条件的所有整数a的和为（　　）

    A.﹣3B.﹣8C.﹣13D.﹣17

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，AB是⊙O的直径，AB＝8，点C在⊙O的半径OA上运动，PC⊥AB，垂足为C，PC＝5，PT为⊙O的切线，切点为T．

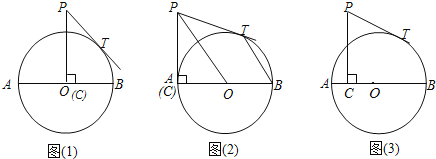
    （1）如图1，当C点运动到O点时，求PT的长；

    （2）如图2，当C点运动到A点时，连接PO、BT，求证：PO∥BT；

    （3）如图3，设PT＝y，AC＝x，求y与x的解析式并求出y的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．

    （1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=　 　°；

    （2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．

    （3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

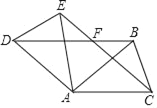
    【题目】如图，已知△ABC中，AB＝AC，把△ABC绕A点顺时针方向旋转得到△ADE，连接BD，CE交于点F．

    （1）求证：△AEC≌△ADB；

    （2）若AB＝，∠BAC＝45°，当四边形ADFC是菱形时，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，对角线的垂直平分线与相交于点，与相交于点，连接。

    （1）求证：四边形是菱形；

    （2）若，求的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从﹣4，﹣3，﹣2，﹣1，0，1，3，4，5这九个数中，随机抽取一个数，记为a，则数a使关于x的不等式组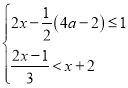至少有四个整数解，且关于x的分式方程＝1有非负整数解的概率是（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，过点（﹣4，0），（0，﹣2）．

    （1）求抛物线的解析式和顶点坐标；

    （2）当﹣4＜x＜4时，求y的取值范围．

    查看答案和解析>>

    同步练习册答案