
【题目】解不等式组 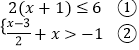 ;并写出解集中的整数解.
;并写出解集中的整数解.
【答案】解:解不等式组 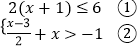 ;
;
解不等式①得:x≤2,
解不等式②得:x> ![]() ,
,
∴不等式组的解集为: ![]() <x≤2;
<x≤2;
∴整数解为:1,2.
【解析】一般先求出其中各不等式的解集,然后依据同大取大;同小取小;大小小大中间找;大大小小找不到确定出不等式组的解集,最后,再找出不等式组的整数解即可.
【考点精析】根据题目的已知条件,利用一元一次不等式组的解法和一元一次不等式组的整数解的相关知识可以得到问题的答案,需要掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.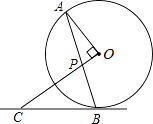
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为 ![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
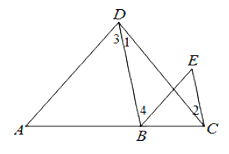
【题目】按图填空,并注明理由.
已知: 如图,∠1=∠2,∠3=∠E. 求证:AD∥BE.
证明: ∵∠1=∠2 (已知)
∴ BD ∥ ( )
∴ ∠E = ( )
又 ∵ ∠E=∠3 ( 已知 )
∴ ∠3=∠ ( )
∴ AD∥BE.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的1号教学大楼共有4道门,其中两道正门大小相同,两道侧门也大小相同,安全检查时,对4道门进行了测试,当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生,当同时开启一道正门和一道侧门时,4分钟内可通过800名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)该中学的2号教学大楼,有和1号教学大楼相同的正门和侧门共5道,若这栋大楼的教室里最多有1920名学生,安全检查规定,在紧急情况下,全大楼学生应在4分钟内通过这5道门安全撤离,该栋大楼正门和侧门各有几道?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某少年宫管、弦乐队共46人.其中管乐队人数少于23人,弦乐队人数不足45人,现准备
购买演出服装.下面是某服装厂给出的演出服装的价格
购买服装的套数 | 1套至23套 | 24套至44套 | 45套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果管乐队、弦乐队分别单独购买服装,一共需付2500元.
(1)管乐队、弦乐队各多少人?
(2)如果管乐队、弦乐队联合起来购买服装.那么比两队各自购买服装共可以节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
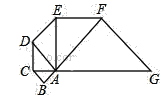
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com