
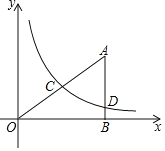
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y��![]() (x��0)��ͼ��AO���е�C����AB�ڵ�D����AD��3��
(x��0)��ͼ��AO���е�C����AB�ڵ�D����AD��3��
(1)���A������Ϊ(4��4)���C������Ϊ�� ����
(2)����D������Ϊ(4��n)��
����������y��![]() �ı���ʽ��
�ı���ʽ��
����C��D�����ֱ������Ӧ�ĺ�������ʽ��
(3)��(2)�������£����E���߶�CD�ϵĶ���(�����C��D�غ�)������E��ƽ��y���ֱ��l�뷴����������ͼ���ڵ�F�����OEF��������ֵ��
���𰸡�(1)C(2��2)��(2)�ٷ�������������ʽΪy��![]() ����ֱ��CD�Ľ���ʽΪy����
����ֱ��CD�Ľ���ʽΪy����![]() x+3��(3)m��3ʱ��S��OEF������ֵΪ
x+3��(3)m��3ʱ��S��OEF������ֵΪ![]() .
.
��������
��1�������е����깫ʽ���ɵó����ۣ�
��2������ȷ������A���꣬�����ó���C���꣬����C��D������뷴���������м��ɵó����ۣ�
����n=1�������C��D���꣬���ô���ϵ�������ɵó����ۣ�
��3�������E���꣬������ʾ����F���꣬���ɽ��������m�ĺ�����ϵʽ���ɵó����ۣ�
(1)�ߵ�C��OA���е㣬A(4��4)��O(0��0)��
��C![]() ��
��
��C(2��2)��
�ʴ�Ϊ(2��2)��
(2)����AD��3��D(4��n)��
��A(4��n+3)��
�ߵ�C��OA���е㣬
��C(2��![]() )��
)��
�ߵ�C��D(4��n)��˫����![]() �ϣ�
�ϣ�
��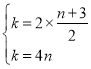 ��
��
��![]() ��
��
�෴������������ʽΪ![]() ��
��
������֪��n��1��
��C(2��2)��D(4��1)��
��ֱ��CD�Ľ���ʽΪy��ax+b��
��![]() ��
��
��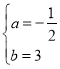 ��
��
��ֱ��CD�Ľ���ʽΪy����![]() x+3��
x+3��
(3)��ͼ����(2)֪��ֱ��CD�Ľ���ʽΪy����![]() x+3��
x+3��
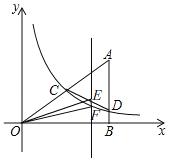
���E(m����![]() m+3)��
m+3)��
��(2)֪��C(2��2)��D(4��1)��
��2��m��4��
��EF��y�ύ˫����![]() ��F��
��F��
��F(m��![]() )��
)��
��EF����![]() m+3��
m+3��![]() ��
��
��S��OEF��![]() (��
(��![]() m+3��
m+3��![]() )��m��
)��m��![]() (��
(��![]() m2+3m��4)����
m2+3m��4)����![]() (m��3)2+
(m��3)2+![]() ��
��
��2��m��4��
��m��3ʱ��S��OEF������ֵΪ![]()




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
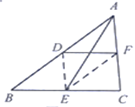
����Ŀ����������ABCD�У�AC�ǶԽ��ߣ����нϴ��ֱ�����ǰ壬һ��ʼ�վ�����B��ֱ�Ƕ���P������AC���ƶ�����һ�߽�DC�ڵ�Q.
(1)��ͼ�٣�����Q��DC����ʱ�����벢д��PB��PQ�������������ϵ��������֤����
(2)��ͼ�ڣ�����Q����DC���ӳ�����ʱ�����벢д��PB��PQ�����������ϵ����֤����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
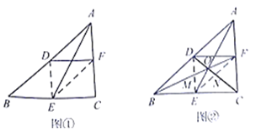
����Ŀ�����̲ij��֣���ͼ�ǻ�ʦ����꼶�ϲ���ѧ�̲ĵ�78ҳ�IJ�������.
��1 ��֤�������ε�һ����λ����������ϵ�������ƽ��.
��֪����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() .
.
��֤��![]() ��
��![]() ����ƽ��.
����ƽ��.
֤��������![]() ��
��![]() .
.
����ݽ̲���ʾ�����ͼ�٣�д�������Ľ������.
������Ӧ�ã���ͼ�ڣ�����ͼ�ٵ�![]() ��
��![]() ���ֱ���
���ֱ���![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() .
.
��1����![]() �����
�����![]() ��
��![]() ֮��ľ���.
֮��ľ���.
��2�����ı���![]() �����Ϊ2����
�����Ϊ2����![]() �����Ϊ______.
�����Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
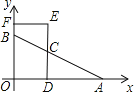
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��4��0������0��2������CΪ�߶�AB������һ�㣨�����A��B�غϣ���CD��OA�ڵ�D����E��DC���ӳ����ϣ�EF��y���ڵ�F������CΪDE�е㣬���ı���ODEF���ܳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��������һ���������Բ����ж��ı���ABCD�Ǿ��ε��� ��������
A.AB��ADB.OA��OBC.AC��BDD.DC��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�DΪб��AB���е㣬��B=60�㣬BC=2cm������E�ӵ�A������AB���B�˶�������F�ӵ�D������������D��C��B�˶���������ٶȾ�Ϊ1cm/s�������յ��ֹͣ�˶�����AE�ij�Ϊx����AEF�����Ϊy����y��x��ͼ�����Ϊ��������
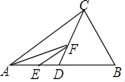
A. 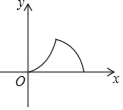 B.
B. 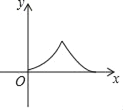
C. 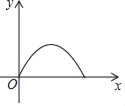 D.
D. 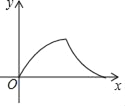
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�
��x�ύ�ڵ�![]() ����
����![]() ����y�ύ�ڵ�C���ҹ���
����y�ύ�ڵ�C���ҹ���![]() ����P��Q��������
����P��Q��������![]() �ϵĶ��㣮
�ϵĶ��㣮
(1)�������ߵĽ���ʽ��
(2)����P��ֱ��OD�·�ʱ����![]() ��������ֵ��
��������ֵ��
(3)ֱ��OQ���߶�BC�ཻ�ڵ�E����![]() ��
��![]() ����ʱ�����Q�����꣮
����ʱ�����Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
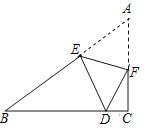
����Ŀ����ͼ��Rt��ABC�У���ACB=90����AC=3��BC=4����E��F�ֱ��ڱ�AB��AC�ϣ�����AEF��ֱ��EF�۵���ʹ��A�Ķ�Ӧ��Dǡ�����ڱ�BC�ϣ�����BDE��ֱ�������Σ���CF�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
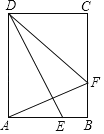
����Ŀ���ھ���ABCD�У�BC��10cm��DC��6cm����E��F�ֱ�Ϊ��AB��BC�ϵ��������㣬E�ӵ�A������ÿ��5cm���ٶ���B�˶���F�ӵ�B������ÿ��3cm���ٶ���C�˶������˶�ʱ��Ϊt�룮����AFD����AED����t��ֵ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com