
Ϊ������ѧ��ҵ��������ҵ��ij��������̨��������ߣ�������Э����������ҵ���ɱ����ṩ��Ʒ����ѧ��ҵ���������ۣ��ɱ����������֮��IJ���������е������������������Ͷ�����۱���������һ�����ͽ��ܵƣ���֪���ֽ��ܵƵijɱ���Ϊÿ��10Ԫ��������Ϊÿ��12Ԫ��ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ��������һ�κ�����y=��10x+500��
��1�������ڿ�ʼ��ҵ�ĵ�һ���½����۵��۶�Ϊ20Ԫ����ô���������Ϊ���е����ܲ��Ϊ����Ԫ��
��2����������õ�����Ϊw��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������
��3����۲��Ź涨�����ֽ��ܵƵ����۵��۲��ø���25Ԫ�����������Ҫÿ�»�õ�������3000Ԫ����ô����Ϊ���е����ܲ������Ϊ����Ԫ��
��1��600����2��30����3��500.
���������������1����x=20����y=��10x+500������۵ļ�����Ȼ����������е��ijɱ����������֮��IJ�ۣ�
��2��������=���ۼ۩��ɱ��ۣ���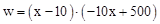 ���Ѻ���ת���ɶ�������ʽ�����ݶ��κ�������������������
���Ѻ���ת���ɶ�������ʽ�����ݶ��κ�������������������
��3���10x2+600x��5000=3000�����x��ֵ�����ͼ���������ķ�Χ��Ȼ����������ÿ����Ϊ���е����ܲ��ΪpԪ������һ�κ�������������ܲ�۵���Сֵ.
�����������1����x=20ʱ��y=��10x+500=��10��20+500=300��
300����12��10��=300��2=600��
�����������Ϊ���е����ܲ��Ϊ600Ԫ.
��2��������ã� ��
��
��a=��10��0���൱x=30ʱ��w�����ֵ4000.
�൱���۵��۶�Ϊ30Ԫʱ��ÿ�¿ɻ���������4000��
��3��������ã���10x2+600x��5000=3000����ã�x1=20��x2=40��
��a=��10��0�������߿������£�
����ͼ���֪����20��x��40ʱ��w��3000.
�֡�x��25���൱20��x��25ʱ��w��3000.
������ÿ����Ϊ���е����ܲ��ΪpԪ��
�� .
.
��k=��20��0����p��x���������С.�൱x=25ʱ��p����Сֵ500.
�����۵��۶�Ϊ25Ԫʱ������ÿ����Ϊ���е����ܲ������Ϊ500Ԫ.
���㣺���κ�����һ�κ�����Ӧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
���壺��һ����Բ�������ߵ�һ���ֺϳɷ��ͼ�Σ����ǰ�������ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ��A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0,8����ABΪ��Բ��ֱ������Բ��Բ��M������Ϊ��1,0������Բ�뾶Ϊ3��
��1������ֱ��д������Բ�������߲��ֵĽ���ʽ ���Ա�����ȡֵ��Χ�� ��
���Ա�����ȡֵ��Χ�� ��
��2�������������C�ġ���Բ��������x��Ľ������ꣻ
��3������D�ġ���Բ�����ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ͼ�������� ��y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��1����������ߵĽ���ʽ��
��2����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ.����CQE��������ʱ�����Q�����ꣻ
��3����ƽ����x��Ķ�ֱ�� ��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ��
��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ�� ��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵������.
��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ��x=��4��x�ύ�ڵ�E��һ�������ϵ������߹�ԭ�㽻�߶�OE�ڵ�A����ֱ��x=��4�ڵ�B����B��ƽ����x���ֱ���������߽��ڵ�C��ֱ��OC��ֱ��AB��D����AD��BD=1��3��
��1�����A�����ꣻ
��2������OBC�ǵ��������Σ���������ߵĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ֱ������ϵxOy�У����κ���y=x2+��2k��1��x+k+1��ͼ����x���ཻ��O��A���㣮
��1����������κ����Ľ���ʽ��
��2�������������ߵĶԳ����ұߵ�ͼ������һ��B��ʹ��AOB���������6�����B�����ꣻ
��3�����ڣ�2���еĵ�B���ڴ����������Ƿ���ڵ�P��ʹ��POB=90�㣿�����ڣ������P�����꣬�������POB��������������ڣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������y��x2��2kx��3k��4��
(1)������y����ʱ��k��ֵΪ_________.
(2)������x����ʱ��k��ֵΪ_________.
(3)�����߾���ԭ��ʱ��k��ֵΪ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪�����߾���A����2��0����B����3��3����ԭ��O������ΪC.
��1���������ߵĺ�������ʽ��
��2���������ߵĶԳ����C�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������ ����һ��M(x0��
����һ��M(x0�� )λ��
)λ�� ���·���
���·���
(1)��֤������������x�ύ�����㣻
(2)����������� ��Ľ���ΪA(
��Ľ���ΪA( ��0)��B(
��0)��B( ��0)����
��0)���� <
< ����֤��
����֤�� <
< <
< ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ������ѧ��ҵ��������ҵ��ij��������̨��������ߣ�������Э����������ҵ���ɱ����ṩ��Ʒ����ѧ��ҵ���������ۣ��ɱ����������֮��IJ���������е������������������Ͷ�����۱���������һ�����ͽ��ܵƣ���֪���ֽ��ܵƵijɱ���Ϊÿ��10Ԫ��������Ϊÿ��12Ԫ��ÿ��������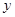 �����������۵���
�����������۵��� ��Ԫ��֮��Ĺ�ϵ��������һ�κ�����
��Ԫ��֮��Ĺ�ϵ��������һ�κ����� ��
��
��1�������ڿ�ʼ��ҵ�ĵ�һ���½����۵��۶�Ϊ20Ԫ����ô���������Ϊ���е����ܲ��Ϊ����Ԫ��
��2����������õ�����Ϊ ��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������
��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������
��3����۲��Ź涨�����ֽ��ܵƵ����۵��۲��ø���25Ԫ�����������Ҫÿ�»�õ�������3000Ԫ����ô����Ϊ���е����ܲ������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com