
分析 (1)先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据P1、P2两点的横坐标判断出两点所在的象限,故可得出结论.
(2)根据题意求得-n=2m,根据勾股定理求得m=1,n=-2,得到P(1,-2),即可得到-k2-1=-2,即可求得k的值,然后分两种情况借助反比例函数和正比例函数图象即可求得.
解答 解:(1)∵-k2-1<0,
∴反比例函数y=$\frac{-{k}^{2}-1}{x}$在每一个象限內y随x的增大而增大,
∵-$\frac{1}{2}$<$\frac{1-\sqrt{3}}{2}$<0,
∴y1>y2;
(2)点P(m,n)在反比例函数y=$\frac{-{k}^{2}-1}{x}$的图象上,m>0,
∴n<0,
∴OM=m,PM=-n,
∵tan∠POM=2,
∴$\frac{PM}{OM}$=$\frac{-n}{m}$=2,
∴-n=2m,
∵PO=$\sqrt{5}$,
∴m2+(-n)2=5,
∴m=1,n=-2,
∴P(1,-2),
∴-k2-1=-2,
解得k=±1,
①当k=-1时,则不等式kx+$\frac{{k}^{2}+1}{x}$>0的解集为:x<-$\sqrt{2}$或0<x<$\sqrt{2}$;
②当k=1时,则不等式kx+$\frac{{k}^{2}+1}{x}$>0的解集为:x>0.
点评 本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式;也考查了反比例函数和一次函数的交点.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
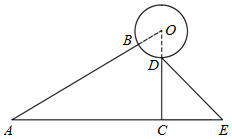 某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
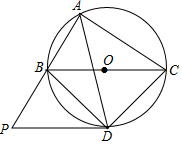 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
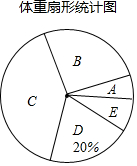 某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:| 组边 | 体重(千克) | 人数 |
| A | 45≤x<50 | 12 |
| B | 50≤x<55 | m |
| C | 55≤x<60 | 80 |
| D | 60≤x<65 | 40 |
| E | 65≤x<70 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 第几次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 比赛成绩 | 145 | 147 | 140 | 129 | 136 | 125 |
| A. | 137、138 | B. | 138、137 | C. | 138、138 | D. | 137、139 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com