
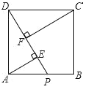
【题目】如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=5,CF=9,则EF=_______.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
3 km | 10 km | -4 km | -3 km | -7 km |
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)该驾驶员离公司距离最远是多少千米?
(3)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店今年1月份的销售额是2万元,3月份的销售额是3.38万元.
(1)求从1月份到3月份,该商店销售额平均每月的增长率;
(2)如果该商店4月份销售额增长率保持不变,销售额能否达到4.5万元,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种竹制躺椅如图①所示,其侧面示意图如图②③所示,这种躺椅可以通过改变支撑杆CD的位置来调节躺椅舒适度.假设AB所在的直线为地面,已知AE=120 cm,当把图②中的支撑杆CD调节至图③中的C′D的位置时,∠EAB由20°变为25°.
(1)你能求出调节后该躺椅的枕部E到地面的高度增加了多少吗?(结果精确到0.1 cm,参考数据:sin 20°≈0.342 0,sin 25°≈0.422 6)
(2)已知点O为AE的一个三等分点,根据人体工程学,当点O到地面的距离为26 cm时,人体感觉最舒适.请你求出此时枕部E到地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
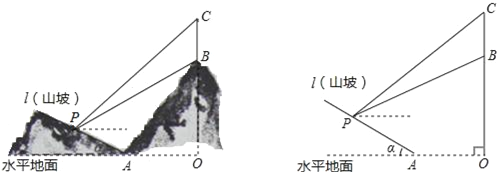
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长10cm,宽8cm的长方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使无盖长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)如果把长方形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的侧面积(指的是高为剪去的正方形边长的长方体的侧面积)可以达到30cm2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com